基本介紹
- 中文名:收斂性
- 外文名:astringency
- 拼音:shōuliǎnxìng
- 全程:隨機變數序列收斂性
- 常見收斂性:依分布收斂、依機率收斂等
- 範疇:數學名詞
定義
常見收斂性
依分布收斂
依機率收斂
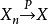
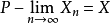
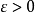
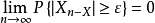
以機率1收斂
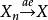
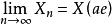
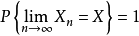
均方收斂
收斂性研究
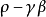
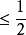
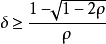
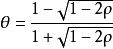
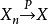
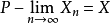
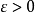
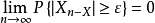
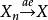
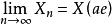
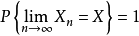
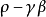
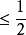
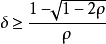
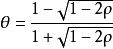
數學分析的基本概念之一,它與“有確定的(或有限的)極限”同義,“收斂於……”相當於說“極限是……(確定的點或有限的數)”。在一些一般性敘述中,收斂和收斂...
上圖收斂性(epigraph convergence)是最最佳化逼近理論中的收斂性質。大部分非線性規划算法只有在目標函式和約束條件函式表達式明顯給出,且其逐次疊代過程中在各疊代點處...
收斂性思維( convergent thinking) 亦稱“輻合性思維”、“求同性思維”。通過分析、綜合、比較、判斷和推理選擇出最有價值構想的一種有方向、有範圍、有條理的思維...
路由協定的收斂性, 網路收斂性 含義 路由器運行相同精確的路由信息 路由收斂的含義是指網際網路中所有路由器運行著相同的、精確的、足以反映當前網際網路拓撲結構的路由...
B收斂性(B-convergence)剛性問題數值方法整體誤差應滿足的一種性質.對剛性問題類了。...
機率收斂性(convergence in probability)是隨機圖的性質,指一種在機率意義下的收斂性。...
一致收斂性是函式列或函式項級數的一種性質。一致收斂函式的判別方法有很多種,最常見的有Cauchy判別法、Abel判別法、Dirichlete判別法等。一致收斂函式具有連續性、...
差分格式收斂性(convergence of a finte difference scheme)偏微分方程數值解法概念之一指差分方程解與其所近似的微分方程解之間的關係.令(二,t)是差分方程求解...
中國區域經濟成長收斂性分析是一篇政治經濟學專業的博士論文,作者管曉明,就讀於南開大學。...
哈納克收斂性定理(Harnack convergence the- orem)調和函式的重要性質.設{u,}在區域口中 是一個單調增加的調和函式序列,並設對某點yE 口,序列{un}y)}有界,...
《中國縣域經濟巨觀管理中經濟成長差異及其收斂性研究》是一篇博士論文,主要對中國縣域經濟的發展作出分析,得出結論,並提出一些建設性意見。...
收斂性質(convergence property)位勢論中的一個概念。...... 收斂性質(convergence property)位勢論中的一個概念。所謂收斂性質,是指在一定條件下單調增加的調和函式...
隨機變數序列收斂性( convergence of sequenceof random variable)“收斂性”的全稱。與函式序列的收斂性不同,隨機變數序列的收斂性總是在一定的機率意義下定義的。...
函式列的收斂性到隨機變數列的推廣。與函式列的收斂性不同,隨機變數列的收斂性是在慨率意義下的收斂性。最常用的是:依分布收斂、依機率收斂,以機率1收斂和r階...
網路收斂性是由於一個路由項的改變,網路中的所有結點全部更新它們的路由表所需時間。...
1 起源 2 收斂性證明 3 另外形式 4 計算方法 5 套用 自然常數起源 編輯 e,作為數學常數,是自然對數函式的底數。有時稱它為歐拉數(Euler number),以瑞...
無窮級數是研究有次序的可數或者無窮個數函式的和的收斂性及和的數值的方法,理論以數項級數為基礎,數項級數有發散性和收斂性的區別。只有無窮級數收斂時有一個和...
1 信賴域算法的基本思想 2 信賴域方法思想 3 信賴域半徑的選擇 4 信賴域算法的步驟 5 信賴域算法的收斂性 信賴域算法信賴域算法的基本思想 編輯 在...
鞣質具收斂性,內服可用於治療胃腸道出血,潰瘍和水瀉等症;外用於創傷、灼傷,可使創傷後滲出物中蛋白質凝固,形成痂膜,可減少分泌和防止感染,鞣質能使創面的微血管...
強性逼近,是一種特殊的函式逼近方式,起源於數項級數的強性求和。...... 強性逼近的另一種問題是對於正數列 ,考慮的收斂性與函式f 的構造性之間的關係。...
其實“時滯”現象早巳對四維時空觀進行了衝擊,愛因斯坦自已也沒有對“時間的膨脹”解釋清楚,只是在粒速小於光速與牛頓力學(引力收斂性)公式相似的現象中被掩蓋了...
例如數列與級數,一致收斂性和廣義積分等,儘量做到所選內容是數學分析的核心問題,避免出現後繼課程將要討論的課題。與一般數學分析教材不同的是,《數學分析》可作為...
