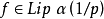強性逼近

強性逼近，是一種特殊的函式逼近方式，起源於數項級數的強性求和。

基本介紹

• 中文名：強性逼近
• 外文名：strong approximation
• 適用範圍：數理科學

簡介

強性逼近是源於級數強性求和的一種逼近。

設為f 的傅立葉級數的前 n+1 項之和，20世紀60年代，亞歷克西茨首先考慮當n→∞時，量

的階與 f(x) 的構造性之間的關係問題，此即所謂強性逼近問題。

套用

一些結果表明，某些逼近定理是可以強化的，例如對於，則費耶爾和的逼近定理

可以強化為

瓦萊·普桑和逼近定理可以強化為

這裡 p>0，C_p是僅與 p 有關的正數，是n階三角多項式對f的最佳逼近值。至於逆命題，則有：對p≥1，

而對0<p<1，則有僅與p有關的正數C_p，使得

另一定義

強性逼近的另一種問題是對於正數列，考慮

的收斂性與函式f 的構造性之間的關係。

例如，當p>1時，由不等式

可推出，而當 0<p≤1是，如記(1/p)=r+α，其中r≥0為整數，0≤α<1，則當0<α<1時，由不等式(1)可推出；當α=0時，由不等式(1)可推出 是亞光滑函式，即有常數C>0，使得對一切 x和h都有