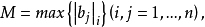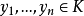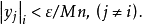逼近定理

逼近定理是不同的賦值之間相互獨立的定理，是中國剩餘定理(孫子定理)的推廣。該定理斷言：若φ₁，φ₂，…，φ_n是域F的互不等價的非平凡賦值，a₁，a₂，…，a_n為F中任意元素，則對於任意ε>0，總存在F中元素x使φ_i(x-a_i)<ε對i=1，2，…，n均成立。

基本介紹

• 中文名：逼近定理
• 外文名：approximation theorem
• 所屬領域：數理科學
• 屬性：賦值的基本定理
• 相關概念：賦值、孫子定理等

基本介紹

逼近定理揭示出不等價的有限個賦值是相互獨立的，這是孫子定理的推廣，在處理多個賦值時將很重要。

逼近(approximation)定理 設 是域K的互不等價的非平凡賦值，記 對K中任意元素 任給 ，必存在K中元素x使得

現若 為有理數域， 是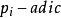 賦值，相應指數賦值記為對任意 任取，則由上述定理有x使

這意味著

即 ，故逼近定理是孫子定理的推廣，下面可看到，二者的證明思路也類似。

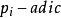
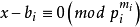
引理1及其證明

引理1 設 如定理1，則存在 使

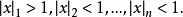
證明:對n歸納，當n=2時，存在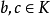使

(因為T₂不強於T₁，T₁也不強於T₂)；故取即可，現設引理1對n-1成立，取使

再取使

若則取即可(m適當大)，現設，對任一賦值若則(對拓撲)，從而從而同樣若，則從而

從而故取即可(m充分大)。

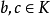
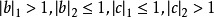
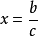
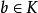
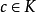
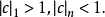
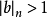
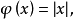
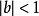
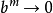
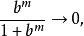
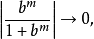
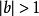
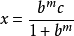
引理2及其證明

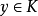引理2設如定理1，任給，存在使

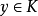
證明:取x如引理1，令

其中m待定，則對，有而

故m充分大時，y滿足引理2。

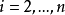
逼近定理的證明

取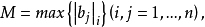由引理2知存在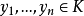使

故滿足定理。