近於一致收斂是一致收斂概念的推廣。設{fn(x)}為定義在可測集E上的可測函式列,對任意σ>0,若存在可測子集A⊂E,使m(A)<σ,在E\A上{fn(x)}一致收斂於f(x),則稱{fn(x)}在E上近於一致收斂於f(x),或說{fn(x)}在E上幾乎一致收斂於f(x)。
基本介紹
- 中文名:近於一致收斂
- 外文名:nearly uniform convergence
- 適用範圍:數理科學
簡介
套用
一致收斂








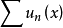

近於一致收斂是一致收斂概念的推廣。設{fn(x)}為定義在可測集E上的可測函式列,對任意σ>0,若存在可測子集A⊂E,使m(A)<σ,在E\A上{fn(x)}一致收斂於f(x),則稱{fn(x)}在E上近於一致收斂於f(x),或說{fn(x)}在E上幾乎一致收斂於f(x)。








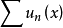

近於一致收斂是一致收斂概念的推廣。設{fn(x)}為定義在可測集E上的可測函式列,對任意σ>0,若存在可測子集A⊂E,使m(A)<σ,在E\A上{fn(x)}一致...
一致收斂是高等數學中的一個重要概念,又稱均勻收斂。一致收斂是一個區間(或點集)相聯繫,而不是與某單獨的點相聯繫。除了柯西準則和餘項準則外,還可以通過...
一致收斂性是函式列或函式項級數的一種性質。一致收斂函式的判別方法有很多種,最常見的有Cauchy判別法、Abel判別法、Dirichlete判別法等。一致收斂函式具有連續性、...
一致收斂判別法是判定函式列與函式項級數是否收斂的重要方法,其中比較著名的有柯西準則、魏爾斯特拉斯判別法以及阿貝爾判別法等,它們是數學分析中重要的理論基礎。...
近幾十年來拓撲空間理論仍在繼續發展,不斷取得新的成果。 [2] 一致收斂拓撲一致空間 編輯 一致空間又叫一致結構。是集合上的一種結構。設X為集合,U為X×X的...
論的部分基本概念間關係所做的三條概括性總結:1.每個(可測)集近於區間的有限並;2.每個(可測)函式近於連續函式;3.每個收斂的(可測)函式序列近於一致收斂。...
例如,可測函式類對於四則運算封閉,對於極限運算封閉,幾乎處處收斂的可測函式列是近於一致收斂的,也即葉戈羅夫定理成立。[2] 伯克霍夫遍歷定理可測空間 編輯 測度...
例如,可測函式類對於四則運算封閉,對於極限運算封閉,幾乎處處收斂的可測函式列是近於一致收斂的,也即葉戈羅夫定理(參見本卷《實變函式論》中的相關條目)成立。 [...
也可以引進平均收斂等概念,並且與幾乎處處收斂、依測度收斂、近於一致收斂的關係也一樣,僅需做明顯的文字和記號修改。中文名 抽象積分 外文名 abstract integral ...
4.3.1幾乎處處收斂與近一致收斂...844.3.2依測度收斂和幾乎處處收斂...864.3.3可測函式的構造...89 習題4...91第5章Lebesgue積分.....
