伯克霍夫遍歷定理

伯克霍夫遍歷定理(Birkhoff ergodic theorem)是遍歷論的第一個重要結果。遍歷理論是研究保測變換的漸近性態的數學分支。它起源於為統計力學提供基礎的"遍歷假設"研究，並與動力系統理論、機率論、資訊理論、泛函分析、數論等數學分支有著密切的聯繫。

基本介紹

• 中文名：伯克霍夫遍歷定理
• 外文名：Birkhoff ergodic theorem
• 領域：數學
• 學科：遍歷論
• 提出者：伯克霍夫
• 函式：可測函式

概念

伯克霍夫遍歷定理(Birkhoff ergodic theorem)是遍歷論第一個重要結果。設(X，A，μ，T)是一個保測系統(即T為保測變換)，一個可測函式f：X→R代表對系統的一種測量，{f(x)，f(Tx)，…}給出了軌道{x，Tx，…}的一種信息。在統計力學、資訊理論中，一個重要問題就是f隨時間的平均值的極限：

是否存在。伯克霍夫(G.D.Birkhoff)針對此問題證明了下述定理，即伯克霍夫遍歷定理：設(X，A，μ)為機率空間，T：X→X為保測變換，則有如下結論：

1.若f∈L¹(X)，則：

μ幾乎處處存在。

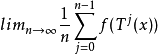
2.若f∈L(X)，1≤p≤+∞，則：

亦屬於L^p(X)且：

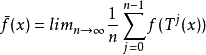
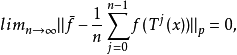
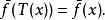
3.對任意f∈L^p(X)，有：

遍歷論

遍歷理論是研究保測變換的漸近性態的數學分支。它起源於為統計力學提供基礎的"遍歷假設"研究，並與動力系統理論、機率論、資訊理論、泛函分析、數論等數學分支有著密切的聯繫。

系統的一個狀態在相空間中有一個代表點P=(p,q），系統的運動就對應於點 P在相空間中的運動。如果系統是保守的，其總能量E便是常數，點P的運動就被限制在相空間中的等能面（稱為能量面）H=E之上。

假如系統的自由度n非常大,例如在一定容器中氣體分子的運動（巨觀上微小的體積中仍含有大量的分子），如果與外界沒有能量交換，就是一個保守的力學系統。這時 n=3N，N是分子的數目。因為人們無法去解如此巨大數目的哈密頓方程組，也無法實際地測得解方程時所必需的初始資料，所以不可能再用純經典力學的方法來研究這樣的系統。其實，系統中大量分子運動的綜合作用才決定出系統的巨觀性質。例如，氣體的單個分子只是斷續地衝撞容器壁，而大量分子衝撞的綜合平均作用才形成了氣體對器壁的穩定的壓強。

為了研究這類本質上是統計性質的運動規律，人們構想同時考慮都是含有N個粒子，處於同一外部條件之中並且具有同一哈密頓量，但微觀狀態不一樣的一切可能的系統。這些系統在相空間中的代表點就不一樣。這些巨觀條件一樣的一切可能的微觀系統的全體稱為系綜(ensemble）。

L.E.玻耳茲曼，特別是J.W.吉布斯建立了完整的統計系綜方法，類比於流體力學中的劉維爾定理，證明了系綜的機率分布守恆定理。如果用φ_t(P）表示相點P 經過時間t之後在相空間中達到的點，那么φ_t便是相空間的一個變換。所謂機率守恆，就是說φt能使一定的機率測度保持不變。

如果某系綜相應的機率分布不顯含時間，就稱做穩定系綜。統計力學基本假設之一是認為真實的平衡物理系統在某時刻的狀態與其相應的穩定系綜在相空間中的點有相同的機率。

可測函式

可測函式是分析學中討論得最廣的函式類。它有許多等價的定義方式，這裡採用如下定義：設(Ω，F)為可測空間，f(x)是定義在Ω上的實值(或擴充實值)函式。若對任意實數c，恆有{x|f(x)>c}∈F，則f(x)稱為(Ω，F)中的可測函式或Ω上的F可測函式。在這個定義中，條件f(x)>c可用f(x)≥c，f(x)<c，f(x)≤c中任一條件來替代。當F為與特殊的測度相應的可測集類時，相應的可測函式可以冠以這些測度的名稱。例如說f(x)為波萊爾可測函式、勒貝格可測函式等。f(x)在(Ω，F)上可測的充分必要條件是，對於直線上的任何波萊爾集M，f(M)是可測集，即f(M)∈F.勒貝格可測函式的概念是由勒貝格(H.L.Lebesgue)於1902年引入的，拉東(J.Radon)於1913年把它推廣到一般的可測空間。除一些涉及R中的特殊拓撲性質(如盧津定理)外，可測空間中的可測函式的性質與勒貝格可測函式的性質基本相同。例如，可測函式類對於四則運算封閉，對於極限運算封閉，幾乎處處收斂的可測函式列是近於一致收斂的，也即葉戈羅夫定理成立。

可測空間

測度的定義域，測度論中的基本概念。設F是基本空間Ω上的σ代數，稱(Ω，F)為可測空間，而稱F中的元素A是(Ω，F)中的可測集，也稱為Ω中的F可測集，簡稱可測集。例如，當F是R中的波萊爾集類B時，(R，B)稱為波萊爾可測空間。當F是R中的勒貝格可測集類L時，(R，L)稱為勒貝格可測空間。可測空間是測度的定義域，在一個可測空間上可以定義不止一種測度。

人物簡介——伯克霍夫

美國數學家。生於普林斯頓，早年在哈佛大學和英國劍橋大學就讀，1932年獲哈佛大學學士學位，後獲理學博士學位。1936年起，任教於哈佛大學，1938—1941年，為助理教授，1941—1946年，為副教授，1946—1982年，任數學教授，1982年退休.美國全國科學院、美國藝術與科學學院院士。1958年，任美國數學會副主席；1971—1972年，任美國數學協會副主席；1967—1968年，任美國工業與套用數學會主席。

伯克霍夫的工作涉及格論、近世代數、核反應堆理論的流體動力學、聲學、偏微分方程的數值解，以及科學計算。他曾和菲力普斯(Phillips，R.S.)定義了取值於局部凸拓撲線性空間的函式的積分.他在1940年出版的《格論》，經重新組織並增擴內容於1967年出版了第三版，除全面闡述了有關理論外，還介紹了格論在分析、集合論(包括拓撲和測度論)等方面的套用，還涉及了有序系統及二進制運算等。他在把代數方法以及其他一些高水準的數學方法套用到別的科學領域方面有重要貢獻，並因此曾於1978年獲美國數學會G.D.伯克霍夫套用數學獎。他一生髮表學術論文近200篇，著有《流體動力學》(1950)、《橢圓方程的數值解》(1971)、《近世代數概論》(1941，與麥克萊恩(MacLane，S.)合著)和《代數》(1967)等專著。