測度論是研究一般集合上的測度和積分的理論。它是勒貝格測度和勒貝格積分理論的進一步抽象和發展,又稱為抽象測度論或抽象積分論,是現代分析數學中重要工具之一。 測度理論是實變函式論的基礎。
基本介紹
- 中文名:測度論
- 外文名:measure theory
- 涉及領域:數學
- 學科:集合論
- 研究內容:測度和積分
- 意義:實變函式論的基礎
定義,形成意義,定理的形成,意義,數學定義,發展歷程,相關定理,環和σ代數,空間函式,測度空間,收斂,平均值,延拓值,
定義
形成意義
定理的形成
縱觀勒貝格積分和勒貝格-斯蒂爾傑斯積分理論,不難發現它們都有三個基本要素。 測度論
測度論
 測度論
測度論第一,一個基本空間(即n維歐幾里得空間R)以及這個空間的某些子集構成的集類即L(勒貝格)可測集或某L-S(勒貝格-斯蒂爾傑斯)可測集全體,這個集類對集的代數運算和極限運算封閉。
第二,一個與這個集類有關的函式類(即L可測函式或某L-S可測函式全體)。
第三,一個與上述集類有關的測度(即L測度或某L-S測度)。
意義
對於更一般的集合,我們能不能定義測度呢? 比如直線上所有有理數構成的集合,它的測度怎么衡量呢?
一個簡單的辦法, 就是先在每個有理點上找一個開區間覆蓋它,就好比給它帶個“帽子”。因為有理數集是可列集(就是可以像排自然一樣排好隊,一個個數出來,也叫可數集,見集合論),所以我們可以讓第n個有理數上蓋的開區間長度是第一個有理數(比方是1)上蓋的開區間長度的2^n分之一。 這樣所有那些開區間的長度之和是個有限值(就是1上的開區間長度的2倍)。
我們讓1上的開區間逐漸縮小趨向於一個點,那么所有區間的總長度也相應縮小,趨向於長度0。 這樣我們就說有理數集的測度是0。 用上面這種方法定義的測度也叫外測度。 測度論
測度論
 測度論
測度論一個幾何區域有了測度,我們就可以定義上面的函式的積分,這是推廣的黎曼積分。
比如實數上的狄利克雷函式D(x)=1(如果x是有理數),0(如果x是無理數)。 如果按照通常的理解,我們發現狄利克雷函式在整個數軸上的定積分不存在;但是按照上面講的有理數的測度,我們就可以求出它的定積分是0。
實直線上的測度如下給出:
設E是實數集,考慮可數個區間(aj,bj)滿足對任何x∈E,都有某個j,使得x∈(aj,bj);考慮所有情形下和(b1-a1)+(b2-a2)+..的下確界稱為E的外測度
如果對任何集合F都有E∩F和F\E的外測度之和等於F的外測度,稱E可測,定義其測度等於外測度
直觀含義上面已經解釋過了
數學定義
測度的相關數學定義:
集函式:設Ψ是上的非空集合類。若對於每一個A∈Ψ,都有一個實數或者±∞之一與之對應(為確定起見,下面假定只取+∞),記為φ(A),且至少有一個A∈Ψ,使得φ(A)取有限值,稱φ(A)為定義在Ψ上的集函式。
(1)若對任意的正整數n以及任意的Ai∈Ψ,i=1,2……,n,Ai∩Aj=O;(i≠j),且(A1∪A2∪…Ai∪…An)∈Ψ,有:
φ(A1∪A2∪…Ai∪…An)=∑[φ(A1)∪φ(A2)∪…φ(Ai)∪…φ(An)],
則稱φ在Ψ上具有有限可加性,也稱φ是Ψ上的有限可加集函式。
(2)若對可列集的Ai∈Ψ,i=1,2……,n,Ai∩Aj=O;(i≠j),且(A1∪A2∪…Ai∪…A∞)∈Ψ,有
φ(A1∪A2∪…Ai∪…A∞)=∑[φ(A1)∪φ(A2)∪…φ(Ai)∪…φ(A∞)],
則稱φ在Ψ上具有完全可加性或者б-可加性,也稱φ是Ψ上的б-可加集函式或者廣義測度。
(3)若對每一個A∈Ψ,φ(A)都取有限值,則稱φ為上的有限集函式。如果對每一個A∈Ψ,存在一個集合序列⊂Ψ,使得
A⊂(A1∪A2∪…Ai∪…A∞),φ(An)<+∞,n=1,2,……
則稱φ是Ψ上的б-有限集函式。
發展歷程
若爾當(Jordan,M.E.C.)於1892年在R中發展了佩亞諾可測集的概念。原來定義外測度時,要用多邊形去覆蓋點集,他規範為用有限個開區間去覆蓋,其餘不變。若爾當的改進使測度概念前進了一大步,蘊涵了勒貝格測度的萌芽,但仍有明顯的缺點。主要是它仍只具有有限可加性,從而導致有些簡單的點集也不可測。例如,令A=[0,1]∩Q,則A的若爾當內測度為0,而外測度為1,因而A在若爾當意義下不可測。總之,若爾當測度只適合於黎曼積分的需要。波萊爾(Borel,(F.-É.-J.-)É.)於1898年,先由開集經過可列並與余的運算導致一類集,即所謂波萊爾集類。再對每個有界波萊爾集對應一個實數,即波萊爾測度,並使得這種測度具有可列可加性。波萊爾的這種思想對測度理論做出了重大貢獻,成為近代測度論中用公理方式引出σ代數概念的起源,並為勒貝格(Lebesgue,H.L.)的工作開闢了道路.波萊爾的學生勒貝格在前人工作的基礎上,於1902年以更一般的形式建立起比較完善的測度理論.他在定義點集測度的方法上,容許可列覆蓋,使所建立的測度具有可列可加性,並且相當廣泛的一類點集的測度有了定義。勒貝格測度是現代抽象測度的起源,在它的基礎上建立的勒貝格積分,是現代分析中套用最廣和意義重大的積分。卡拉西奧多里(Carathéodory,C.)於1914年發展了外測度理論,對測度進行了公理化研究,並給出了測度擴張的典型方法,成為近代測度論的基礎.拉東(Radon,J.)、薩克斯(Saks,S.)、弗雷歇(Fréchet,M.-R.)以及另外一些人考慮了一般集合上的測度以及測度空間的乘積,並建立了一般可測集上積分的理論。
一般集合上的測度和積分理論是最廣泛的測度理論,但為適應各方面的需要,還出現了其他種種特殊的測度和積分.例如,20世紀30年代初,伴隨著人們對取值於巴拿赫空間的函式性質特別是可微性和可積性的研究,出現了有關向量值測度的一些工作。1960年以後,向量值測度理論得到蓬勃發展,並逐漸趨於完善。又如,19世紀建立的傅立葉分析理論,對於套用數學而言,當時已是令人滿意的數學工具,但由於黎曼積分的局限性,對於函式與展開式之間的關係,直到勒貝格積分理論確立之後才有深刻的揭示.勒貝格積分的出現對於傅立葉展開的研究顯然促進了一大步,但依舊顯示出了它的局限性。研究拓撲群上的測度是建立群上傅立葉分析的基本問題之一,這個問題自1930年以來,經過哈爾(Haar,A.)、韋伊(Weil,A.)和蓋爾范德(Гельфанд,И.М.)等人的工作而趨於完善。再如,20世紀初測度論的建立,使得人們對R中的子集關於n維勒貝格測度的性質有了很好的了解。但在處理與R中低維點集有關的數學問題時遇到了困難。在這種背景下,20世紀20年代出現了幾何測度論,它是研究高維空間中低維點集的測度及低維點集上積分的理論。
測度概念與積分概念緊密相關。每一種測度理論的推廣都可導致一種積分理論的推廣.測度理論不僅是積分理論的基礎,而且在現代分析以及機率論等許多數學領域中也有著廣泛的套用。
相關定理
此外,測度還可以取值於任何線性空間(通常帶有一定拓撲,比如Banach空間),只要滿足相應的可數可加性。在Hilbert空間運算元理論中還有所謂譜測度的概念,其中測度的取值為一固定Hilbert空間中投影運算元的全體,且滿足(在強意義下)的可數可加性。
如果測度空間X是拓撲空間而所考慮的б代數(或者б環,後者按照Halmos《Measure Theory》)由全體緊集生成(這定義不是標準的;有的書上說是由全體開集生成),且測度在每個緊集上取有限值,則稱為Borel測度。如果Borel測度限制在所有能寫成可數個開集的交的緊集生成的б環上,則稱為Baire測度。如果任何可測集E滿足
μ(E)=sup{μ(K): K含於E,K緊}=inf{μ(O):O包含E,O開}
則稱μ為正則測度。
環和σ代數
設X是非空的集。E是以Χ的某些子集作為元素構成的集,稱E為Χ上的一個集類。設R是Χ上的一個集類。如果它對集的並、差運算封閉,即對任何A、B∈R,必有A∪B∈R,A\B∈R,則稱R為Χ上的環;如果R不僅是一個環,而且Χ∈R,則稱R為Χ上的代數。例如直線R1上的左開右閉的有限區間(α,b](α=b時,(α,b]表示空集)的全體記為P,P便是R1上的集類,但不是環。P中任意有限個集的並的全體記為R0,R0便是R1上的環,但不是代數。直線上任意有限個區間(包括無限區間)的並的全體R奿是R1上的代數。環或代數雖對集的代數運算(即並、差、交運算)封閉,但對極限運算不一定封閉,這就不適應分析數學的要求。因此,需要引入下面的概念:設φ)是Χ上的一個環,如果它對集的可列並運算封閉,則稱φ為Χ上的σ環;如果φ是σ環,並且Χ∈φ),則稱φ)為Χ上的σ代數。σ環就對集的並、差、交以及極限運算都封閉,而σ代數還對集的求余集運算封閉。例如,R0不是R1上的σ環,而L可測集(或L-S可測集)的全體是R1上的σ代數。又如Χ的一切子集的全體Χ是Χ上的σ代數。由於任意個環的交仍是環,因此對一個集類E,一切包含E的環的交是包含E的最小環,記為R(E)。同樣,包含E的最小σ環記為φ(E)。
空間函式
設φ是Χ 上的σ環,稱(Χ,φ)為可測空間,而稱φ中的任何集A為(Χ,φ)中的可測集(也稱為Χ中的φ可測集)。如果Χ是Rn,而φ分別是Rn中 L可測集全體(記為L)、由單調增加右連續函式g(x)生成的L-S可測集全體(記為 Lg)、波萊爾集全體(記為B),則相應地稱(Χ,φ)是L可測空間、L-S可測空間、波萊爾可測空間。設E是可測空間(Χ,φ))中的可測集,ƒ是定義在E上的有限實值函式。如果對任何實數с,{Χ│ƒ(x)>с}∈φ,那么稱ƒ為E上關於(Χ,φ)的可測函式,也稱為E上的φ)可測函式。這種可測函式是L可測函式、L-S可測函式等概念的直接推廣。它有許多等價定義方式,並且具有L可測涵數所具有的代數性質及極限性質。定義在E上的復值函式ƒ,如果它的實部、虛部都是可測函式,那么就稱ƒ為E上的可測函式。可測空間、可測集、以及可測函式等概念原則上並不涉及測度。
測度空間
設Χ是非空集,E是Χ上的集類,定義在E上的函式稱為集函式(因為自變元是屬於E,它是Χ的子集)。設R是Χ上的環,μ是定義在R上的取非負的廣義實值(可以取值+∞)的集函式,如果滿足:①μ(═)=0(═是空集);②(可列可加性)對任何一列互不相交的 An∈R(n=1,2…,),並且:式①,有:式②=③,則稱μ為環R上的測度。設(Χ,φ)是一個可測空間,μ是定義在φ上的測度,則稱(Χ,φ),μ)是測度空間。特別,(R1,L,m)及(R1,Lg,mg)分別稱為(直線上的)L測度空間和L-S 測度空間。測度空間(Χ,φ,μ)中的測度μ 除了平移、反射不變性以及余集(因為 X可能不在S中)的性質外,具有勒貝格測度m的其他性質。由於φ是σ環,對集的極限運算封閉,所以測度空間是建立具有良好的極限性質的積分的基礎。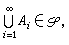 式①
式① ③
③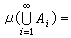 式②
式②
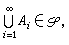 式①
式① ③
③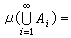 式②
式②設A是可測空間(Χ,φ)中可測集。如果有一列可測集{An},μ(An)<∞(n=1,2,…),使得:式④,則稱A為σ有限集。如果φ)中一切集都是σ有限的,則稱(Χ,φ),μ)是σ有限的測度空間。特別,當φ是σ代數且Χ是σ有限集時,稱(Χ,φ),μ)為全σ有限測度空間。通常分析數學中所用的具體的(Χ,φ),μ)大都是全σ有限測度空間。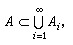 式④
式④
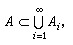 式④
式④設測度空間(Χ,φ),μ)中的φ)是σ代數,如果μ(Χ)<∞,則稱(Χ,φ),μ)為全有限的測度空間。特別,當μ(Χ)=1時,稱(Χ,φ),μ)為機率測度空間(機率論中用的全是這種空間)。
設A是測度空間(Χ,φ),μ)上的可測集。如果μ(A)=0,則稱A為μ零集。如果(Χ,φ),μ)中任何一個μ零集的任何子集都是可測集,則稱(Χ,φ), μ)為完全測度空間。例如(R1,L,m),(R1,Lg,mg)都是完全的、全σ有限的測度空間。
收斂
同L測度一樣,在測度空間(Χ,φ,μ)中也有命題P在E上“幾乎處處”成立的概念,它是指E中使命題P不成立的點的全體(它可能不是可測集)包含在某個μ 零集中。對於完全測度空間,命題P在E上幾乎處處成立就是指使命題 P不成立的點的全體是μ零集。在不完全的測度空間上,關於μ幾乎處處相等的兩個可測函式ƒ和h,未必能從ƒ的可測性推出h也是可測的,只有在完全測度空間才能做到這一點。對於測度空間上的可測函式序列,常用的重要收斂概念同樣有兩個:一是E上可測函式列{ƒn}幾乎處處收斂於可測函式ƒ,即{x│ƒn(x)→ƒ(x)}包含在某個μ零集中;另一是E上可測函式列{ ƒn}度量收斂 (或稱依測度收斂)於可測函式 ƒ,即對任何 ε>0,式⑤,上述兩種收斂的關係是和L測度的情形一樣。此外,在測度空間上也成立葉戈羅夫定理:設E上可測函式列{ƒn}幾乎處處收斂於可測函式ƒ,並且μ(E)<∞ ,則對任何δ>0,必存在可測集Eδ∈E,使得μ(E\Eδ)<δ,且{ƒn}在Eδ上一致收斂於ƒ。類似於L測度的情形,在測度空間上也可引入度量基本序列(或依測度基本序列),並成立相應的完備性定理。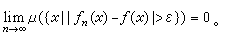 式⑤
式⑤
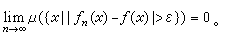 式⑤
式⑤平均值
同 L積分建立過程完全一樣,可以建立測度空間上的積分概念,將那裡的測度m換成μ即可。L積分所具有的大部分性質對一般的測度空間上的積分也是成立的。在測度空間中也有積分平均收斂,平方平均收斂或更一般的p次平均收斂的概念以及相應的性質。
延拓值
對積分來說,採用關於集的極限運算不封閉的環上的測度是不夠的,有用的是σ環上的測度。然而由於環的結構比σ環的結構要簡單得多,所以在環上給出一個測度或驗證環上的某個非負集函式是否是測度往往比在 σ環上要簡單得多。自然就產生定義在環R上的測度是否一定能延拓成包含R的最小σ環φ(R)上的測度的問題。測度論中證明了如下重要定理:任何環上的σ 有限測度必可惟一地延拓成包含它的最小σ 環上的 σ有限測度。

