基本介紹
- 中文名:黎曼積分
- 外文名:Riemann Integral
- 別稱:定積分
- 領域:數學
- 人物:黎曼
概念


 圖1.作為曲線與坐標軸所夾面積的黎曼積分
圖1.作為曲線與坐標軸所夾面積的黎曼積分定義
1.區間的分割





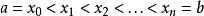

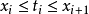



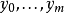



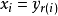


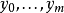



2.黎曼和
 圖2.黎曼積分——黎曼和
圖2.黎曼積分——黎曼和3.黎曼積分

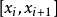



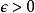



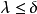












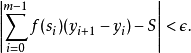





性質
1.線性
2.正定性

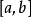

3.可加性



4.其他性質

推廣



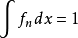
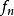

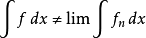

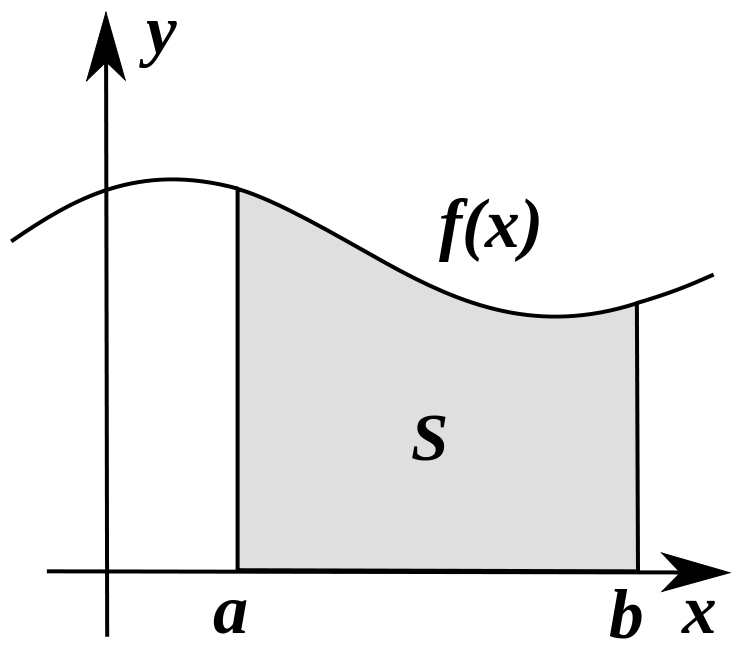


 圖1.作為曲線與坐標軸所夾面積的黎曼積分
圖1.作為曲線與坐標軸所夾面積的黎曼積分




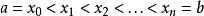

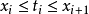



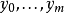



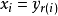


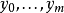



 圖2.黎曼積分——黎曼和
圖2.黎曼積分——黎曼和
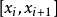



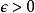



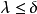












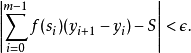






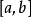








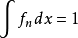
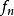

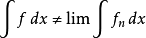

黎曼積分(Riemann Integral),也就是所說的正常積分、定積分。在實分析中,由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上...
這裡有一塊形狀不規則的土地,要測量它的面積,怎么辦呢?一個叫黎曼的德國數學家(Bernhard Riemann, 1826-1866),他想了個辦法:將這不規則圖形切成一條條的小長條...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
勒貝格積分,是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是求其函式圖像與軸之間的面積。...
黎曼-斯蒂爾傑斯積分(英語:Riemann-Stieltjes integral)是一種積分,它是黎曼積分的一種推廣。黎曼-斯蒂爾傑斯積分有數種定義方式,但不是每種定義方式都是彼此等價的...
絕對積分是使函式與其絕對值同時可積的那種積分,否則稱為非絕對積分。...... 黎曼積分是非絕對積分。黎曼積分也就是所說的正常積分、定積分。在實分析中,由黎曼創...
定積分是積分的一種,是函式f(x)在區間[a,b]上積分和的極限。這裡應注意定積分與不定積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),...
數值積分,用於求定積分的近似值。在數值分析中,數值積分是計算定積分數值的方法和理論。在數學分析中,給定函式的定積分的計算不總是可行的。許多定積分不能用已知...
勒貝格積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是函式...
向量值積分,普通(數值的)積分在向量值上的推廣。在分析數學的各分支中,因不同的要求,需要種種或是向量值函式的積分或是關於向量值測度的積分。向量值函式的積分...
逐項積分是微積分術語,即函式列(級數)逐項求積分後與其極限(和)的積分相等,對函式列(級數)的每一項積分,使所得到的序列(級數)收斂於原序列(級數)的極限函式(和...
對一般的條件收斂級數,也可以用以上的算法來證明黎曼級數定理。上文中有關交錯調和級數的算法之所以成立,原因有二:首先,所有正項構成的級數發散到正無窮大,所有負...
勒貝格-斯蒂爾傑斯積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看...
數學上,可積函式是存在積分的函式。除非特別指明,一般積分是指勒貝格積分;否則,稱函式為"黎曼可積"(也即黎曼積分存在),或者"Henstock-Kurzweil可積",等等。黎曼...
