基本介紹
- 中文名:黎曼-斯蒂爾傑斯積分
- 外文名:Riemann-Stieltjes integral
- 內容:R-S積分和L-S積分的統稱。
- 提出者:斯蒂爾傑斯
定義
區間的分割
黎曼-斯蒂爾傑斯和
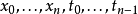




黎曼-斯蒂爾傑斯積分
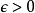





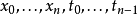
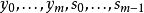


與黎曼積分間的關聯
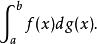
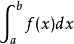
參見
- 有界變差
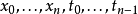




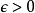





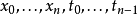
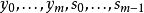


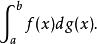
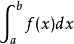
黎曼-斯蒂爾傑斯積分(英語:Riemann-Stieltjes integral)是一種積分,它是黎曼積分的一種推廣。黎曼-斯蒂爾傑斯積分有數種定義方式,但不是每種定義方式都是彼此等價的...
在實分析中,由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上的某些不足之處可由後來的黎曼-斯蒂爾傑斯積分和勒貝格積分...
黎曼-斯蒂爾傑斯(簡記為R-S)積分和勒貝格-斯蒂爾傑斯(簡記為L-S)積分的統稱。...... 黎曼-斯蒂爾傑斯(簡記為R-S)積分和勒貝格-斯蒂爾傑斯(簡記為L-S)積分的統...
勒貝格-斯蒂爾傑斯積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看...
在分析數學的各分支中,因不同的要求,需要種種或是向量值函式的積分或是關於向量值測度的積分。向量值函式的積分有黎曼-斯蒂爾傑斯型積分和勒貝格型積分。...
,是因為其形式為黎曼-斯蒂爾傑斯積分,但在黎曼-斯蒂爾傑斯積分中變數的取值範圍應該還是x的取值範圍,而不是g(x)的取值範圍。參考資料 1. 華中科技大學數學系.微...
黎曼積分的重要推廣,分析數學中普遍使用的重要工具。19世紀的微積分學中已經有了許多直觀而有用的積分,例如黎曼積分(簡稱R積分)、黎曼-斯蒂爾傑斯積分(簡稱R-S積分...
在實分析中,由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上的某些不足之處可由後來的黎曼-斯蒂爾傑斯積分和勒貝格積分...
在實分析中, 由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上的某些不足之處可由後來的黎曼-斯蒂爾傑斯積分和勒貝格積分...
斯蒂爾傑斯最重要的貢獻是推廣了黎曼積分概念。1894年他發表了論文《連分數的研究》,文中提出了在解析函式論和一元實變函式論中本質上是全新的問題,為了表示一個...
斯蒂爾傑斯最重要的貢獻是推廣了黎曼積分概念。在1884年,當斯蒂爾傑斯研究高斯關於某種定積分的近似計算公式時,驚訝地發現連分數與定積分之間的某種奇妙關係.他花費10...
布朗運動的樣本函式雖然連續,但幾乎所有的樣本函式非有界變差,甚至處處不可微,因而無法按樣本函式來定義通常的黎曼-斯蒂爾傑斯積分(簡稱RS積分)或勒貝格-斯蒂爾傑斯...
斯蒂爾傑斯最重要的貢獻是推廣了黎曼積分概念。1894年他發表了論文《連分數的研究》,文中提出了在解析函式論和一元實變函式論中本質上是全新的問題,為了表示一個...
黑利定理是黎曼-斯蒂爾傑斯積分在積分號下取極限的定理。設f(x)是[a,b]上的連續函式,有界變差函式列{gn(x)}在[a,b]上收斂於有限函式g(x),且 則...
11143黎曼-斯蒂爾傑斯積分 11144泛函分析 11145泛函式 11146譜論 11147線性運算元 11148廣義函式 11149變分法 11150大範圍變分法 11151函式逼近論 11152傅立葉分析 1115...
(逝於1898年)1856年(丙辰年):湯姆斯·斯蒂爾吉斯,荷蘭數學家,以黎曼-斯蒂爾傑斯積分聞名。1876年:帕布羅·卡薩爾斯,西班牙作曲家、指揮家。(逝於1973年)...
希爾伯特空間中的線性變換、黎曼夸函式和斯蒂爾傑斯積分概念的發展等方面.他還研究了所謂力矩問題,提出了以他名字命名的有關方法.1921- 1922年,他指出黎曼參函式具有...
