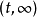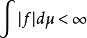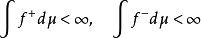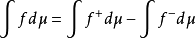勒貝格-斯蒂爾傑斯積分(英語：Lebesgue integral)是現代數學中的一個積分概念，它將積分運算擴展到任何測度空間中。在最簡單的情況下，對一個非負值的函式的積分可以看作是函式圖像與x軸之間的面積。勒貝格積分則將積分運算擴展到更廣的函式（可測函式），並且也擴展了可以進行積分運算的集合（可測空間）。最早的積分運算對於非負值的函式來說，其積分相當於使用求極限的手段來計算一個多邊形的面積（也就是黎曼積分），但這過程需要函式足夠規則。但是隨著對更加不規則的函式的積分運算的需要不斷產生（比如為了討論數學分析的極限過程中導致的函式，或者出於機率論的需求），很快就產生了對更加廣義的求極限手段的要求來定義相應的積分運算。
基本介紹
- 中文名：勒貝格-斯蒂爾傑斯積分
- 外文名：Lebesgue integral
- 學科：數學
引入,推導,測度理論,積分,
引入
在閉區間a和b之間對函式 f的積分可以被看作是 f的函式圖像下的面積。對於多項式這樣比較常見的函式來說這個定義簡而易懂。但是對於更加稀奇古怪的函式來說它是什麼意思呢？廣義地來說，對於什麼樣的函式“函式圖像下的面積”這個概念有意義？這個問題的答案具有很大的理論性和實際性意義。
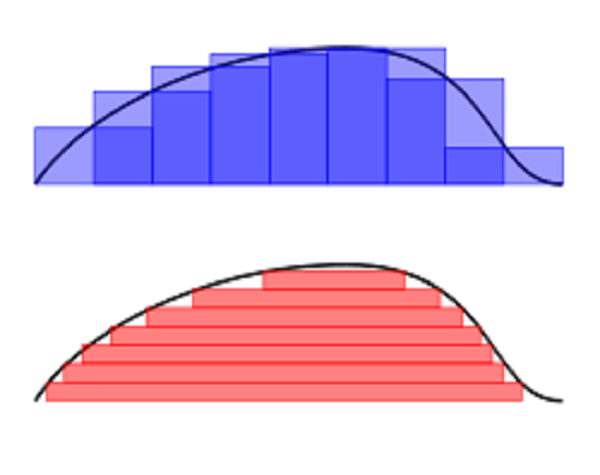
19世紀裡在數學中有把整個數學理論放到一個更加堅固的基礎上的趨勢。在這個過程中數學家也試圖給積分計算提供一個穩固的定義。波恩哈德·黎曼提出的黎曼積分成功地為積分運算提供了一個這樣的基礎。黎曼積分的出發點是構造一系列容易計算的面積，這些面積最後收斂於給定的函式的積分。這個定義很成功，為許多其它問題提供了有用的答案。
但是在求函式序列的極限的時候黎曼積分的效果不良，這使得這些極限過程難以分析。而這個分析比如在研究傅立葉級數、傅立葉變換和其它問題時卻是極其重要的。勒貝格積分能夠更好地描述在什麼情況下積分有極限。勒貝格積分所構造出的容易計算的面積與黎曼積分所構造的不同，這是勒貝格積分更加成功的主要原因。勒貝格的定義也使得數學家能夠計算更多種類的函式的積分。比如輸入值為無理數時函式值為0，輸入值為有理數時函式值為1的狄利克雷函式沒有黎曼積分，但是有勒貝格積分。
推導
以下的介紹是遵循最常見的勒貝格積分的介紹進行的。在這個介紹中積分理論分兩部分：
- 可測集和在這些集合上可以進行的測量的理論
- 可測函式和對這些函式積分的理論
測度理論
最初測度理論是用來對歐幾里得空間中直線的長度，以及更廣義地，歐幾里得空間的子集的面積和體積進行仔細分析發展出來的。它尤其可以為 R的哪些子集擁有長度這個問題提供一個系統性的回答。後來發展的集合論證明，實際上不可能為 R的所有子集都分配一個長度，且保持天然的可加性和平移不變的性質。因此給出一個合適的，可測量的子集類是一個關鍵的前提。
當然，黎曼積分隱含了長度的概念。事實上計算黎曼積分的元素是[a,b]×[c,d]所組成的長方形，它的面積為(b−a)(d−c)。b−a是這個長方形的寬度，而d−c則是其高度。黎曼只能用平面的長方形來估算曲線下的面積，因為當時還沒有其它適當的理論來測量更一般的集合。
在大多數現代的教科書中測度和積分都是公理性的。也就是說測度是一個定義在集合 E的某些子集組成的集合 X上的函式μ，這些子集必須擁有一定的特徵。在許多不同的情況下這些特徵成立。
積分
從一個測度空間(E,X,μ)出發，E是一個集合，X是由 E的子集構成的σ代數，μ是定義在 X上的測度。
在勒貝格理論中只有對所謂的可測函式才能夠進行積分。一個函式f被稱為是可測的，假如每個區間
的的原像是 E中的可測集合，也就是：
若
則 f被稱為勒貝格可積的。在這種情況下，兩個積分均滿足
因此可以定義
