基本介紹
- 中文名:定積分
- 外文名:definite integral
- 學科:數學
- 本質:積分
- 釋義:積分和的極限
- 相關名詞:不定積分
積分分類
 定積分
定積分定義




性質


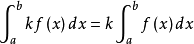
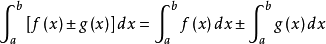



常用積分法
換元積分法


分部積分法

分點問題
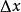
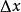
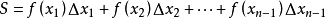
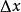
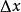





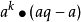







黎曼積分
 定積分
定積分定理

套用
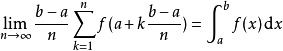



 定積分
定積分











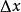
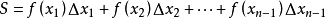
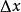
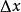





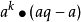







 定積分
定積分
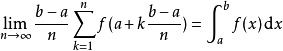


定積分是積分的一種,是函式f(x)在區間[a,b]上積分和的極限。這裡應注意定積分與不定積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),...
在微積分中,一個函式f 的不定積分,或原函式,或反導數,是一個導數等於f 的函式 F ,即F′ = f。不定積分和定積分間的關係由微積分基本定理確定。其中F是f...
積分是微分的逆運算,即知道了函式的導函式,反求原函式。在套用上,積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊三角形的面積,這巧妙的求解方法是積分...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
分部積分法是微積分學中的一類重要的、基本的計算積分的方法。它是由微分的乘法法則和微積分基本定理推導而來的。它的主要原理是將不易直接求結果的積分形式,轉化...
積分表是在積分計算中為了使用與方便,把常用的積分公式匯集成的一種數學用表。積分表是按照被積函式的類型來排列的。求積分時,可根據被積函式的類型直接地或經過...
微積分(Calculus),是高等數學中研究函式的微分(Differentiation)、積分(Integration)以及有關概念和套用的數學分支。它是數學的一個基礎學科。內容主要包括極限、微分學...
黎曼積分(Riemann Integral),也就是所說的正常積分、定積分。在實分析中,由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上...
積分中值定理,是一種數學定律。分為積分第一中值定理和積分第二中值定理,它們各包含兩個公式。其中,積分第二中值定理還包含三個常用的推論。積分中值定理揭示了...
反常積分又叫廣義積分,是對普通定積分的推廣,指含有無窮上限/下限,或者被積函式含有瑕點的積分,前者稱為無窮限廣義積分,後者稱為瑕積分(又稱無界函式的反常積分)...
在數值分析中,數值積分是計算定積分數值的方法和理論。在數學分析中,給定函式的定積分的計算不總是可行的。許多定積分不能用已知的積分公式得到精確值。數值積分是...
換元積分法(Integration By Substitution)是求積分的一種方法,主要通過引進中間變數作變數替換使原式簡易,從而來求較複雜的不定積分。它是由鏈式法則和微積分基本...
定積分概念的推廣至積分區間無窮和被積函式在有限區間上為無界的情形成為廣義積分,又名反常積分。其中前者稱為無窮限廣義積分,或稱無窮積分;後者稱為無界函式的廣義...
極坐標定積分是以R為半徑,θ為積分變元,計算曲線周長的、面積的積分。曲線的周長定積分為,曲線的面積定積分為。設曲線ρ=R在區間[θ1,θ2]上非負連續,當d...
如果上限x在區間[a,b]上任意變動,則對於每一個取定的x值,定積分有一個對應值,所以它在[a,b]上定義了一個函式,這就是積分變限函式。...
積分不等式是微積分學中的一類重要不等式,也為解決微分方程等方面的問題提供了 富有成效的理論工具。主要有楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式等...
二重積分是二元函式在空間上的積分,同定積分類似,是某種特定形式的和的極限。本質是求曲頂柱體體積。重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心等...
定積分的元素法是在套用定積分的理論來分析和解決一些幾何,物理中的問題時,需要將一個量表達成為定積分的分析方法。...
積分符號(Signs for Definite Integrals)是萊布尼茨於1675年以“omn.l”表示l的總和(積分(Integrals)),而omn為omnia(意即所有、全部)之縮寫。其後他又改寫為 ∫...
在數學中,指數積分是函式的一種,它不能表示為初等函式,是特殊的不完全伽馬函式之一。...
積分方程是含有對未知函式的積分運算的方程,與微分方程相對。許多數學物理問題需通過積分方程或微分方程求解。積分方程是近代數學的一個重要分支。數學、自然科學和工程...
《常用積分表》是2009年中國科學技術大學出版社出版的圖書,作者是《常用積分表》編委會 。...
柯西積分公式是一把鑰匙,他開啟了許多方法與定理;他刻畫了解析函式的又一種定義;人們對它的研究極具意義,讓解析函式論能夠單獨脫離於實函式。通過柯西積分公式就...
如果函式f(x,y)在有界閉區域D上連續,區域D的面積為S,且 m 和 M 分別是f(x,y)在D上的最小值和最大值,則mS ≤∫∫f(x,y)在D上的二重積分 ≤ MS...
牛頓-萊布尼茲公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函式的原函式或者不定積分之間的聯繫。牛頓-萊布尼茨公式的內容是一個...
而被稱為萬能公式的原因是利用的代換可以解決一些有關三角函式的積分。參見三角換元法。 [1] 萬能公式三角萬能公式 編輯 1.常用的萬能公式...
