基本介紹
解釋
性質




求解

積分公式















 不定積分
不定積分積分方法
積分公式法
換元積分法
 不定積分
不定積分





分部積分法
 不定積分
不定積分不可積函式

 不定積分
不定積分積分表


示例


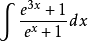





















 不定積分
不定積分 不定積分
不定積分





 不定積分
不定積分
 不定積分
不定積分



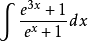

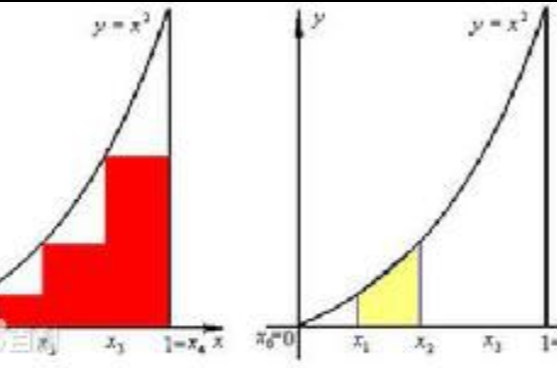
在微積分中,一個函式f 的不定積分,或原函式,或反導數,是一個導數等於f 的函式 F ,即F′ = f。不定積分和定積分間的關係由微積分基本定理確定。其中F是f...
定積分是積分的一種,是函式f(x)在區間[a,b]上積分和的極限。這裡應注意定積分與不定積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),...
不定積分的運算法則,別稱不定積分的性質,f(x)的原函式,存在微分的反函式。...... 不定積分的運算法則,別稱不定積分的性質,f(x)的原函式,存在微分的反函式。...
不定積分的積分公式主要有如下幾類:含ax+b的積分、含√(a+bx)的積分、含有x^2±α^2的積分、含有ax^2+b(a>0)的積分、含有√(a²+x^2) (a>0)...
當儒瓦不定積分廣義當儒瓦可積函式 設f(x)是定義在閉區間[a,b]上的一個實值函式。若存在一般絕對連續函式F(x),使得對於[a,b]中幾乎所有的點,F(x)的近似...
不定積分是微分的逆運算。...... 不定積分是微分的逆運算。所以我們得到一些基本的公式:詞條標籤: 科技術語 , 科學 V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
勒貝格不定積分簡介 編輯 勒貝格積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
積分表是在積分計算中為了使用與方便,把常用的積分公式匯集成的一種數學用表。積分表是按照被積函式的類型來排列的。求積分時,可根據被積函式的類型直接地或經過...
分部積分法是微積分學中的一類重要的、基本的計算積分的方法。它是由微分的乘法法則和微積分基本定理推導而來的。它的主要原理是將不易直接求結果的積分形式,轉化...
換元積分法(Integration By Substitution)是求積分的一種方法,主要通過引進中間變數作變數替換使原式簡易,從而來求較複雜的不定積分。它是由鏈式法則和微積分基本...
如果上限x在區間[a,b]上任意變動,則對於每一個取定的x值,定積分有一個對應值,所以它在[a,b]上定義了一個函式,這就是積分變限函式。...
現行不定積分的定義為:若函式f(x)在某區間 I 上存在一個原函式F(x),則稱F(x)+C(C為任意常數)為f(x)在該區間上的不定積分,記為 。...
狹義當儒瓦不定積分狹義當儒瓦可積函式 狹義當儒瓦可積函式是勒貝格可積函式的推廣。當儒瓦(Denjoy,A.)於1912年給出了狹義當儒瓦積分的定義,它同時成為勒貝格積分和...
有理函式積分法是按一定步驟求有理函式不定積分的方法,求有理函式的積分時,先將有理式分解為多項式與部分分式之和,再對所得到的分解式逐項積分。有理函式的原...
1 定義 2 基本積分表 3 換元積分法 4 分部積分法 積分法定義 編輯 積分法是從已知函式f求其原函式(不定積分)的方法。包括(...
因此,對於證明有關題設中含有某個函式積分的等式或不等式,或者要證的結論中含有定積分,或者所求的極限式中含有定積分時,一般應考慮使用積分中值定理, 去掉積分號...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
二重積分是二元函式在空間上的積分,同定積分類似,是某種特定形式的和的極限。本質是求曲頂柱體體積。重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心等...
極坐標定積分是以R為半徑,θ為積分變元,計算曲線周長的、面積的積分。曲線的周長定積分為,曲線的面積定積分為。設曲線ρ=R在區間[θ1,θ2]上非負連續,當d...
《常用積分表》包含最常用的初等函式和特殊函式的不定積分與定積分公式2552個,另外還有203個積分變換公式.積分公式中遇到的所有函式(包括被積函式和積分後的函式)的...
而被稱為萬能公式的原因是利用的代換可以解決一些有關三角函式的積分。參見三角...2.不常用的萬能公式 [1] [1] [1] 萬能公式導函式公式 編輯 ...
不定積分的換元法解法整體換元 又稱整體換元,是在已知或者未知中,某個代數式幾次出現,而用一個字母來代替它從而簡化問題,當然有時候要通過變形才能發現。例如解...
10 微積分學 ▪ 極限的定義 ▪ 導數 ▪ 曲率 ▪ 不定積分 ▪ 定積分 ▪ 普通分類 11 國小奧數公式 ▪ 植樹問題 ▪ 盈虧問題 ...
