基本介紹
- 中文名:牛頓-萊布尼茨公式
- 外文名:Newton-Leibniz formula
- 分類:數學
- 又名:微積分基本定理
- 時間:1677年
- 提出 :牛頓 萊布尼茨
定理定義
定義




弱化條件






公式推導
推導一




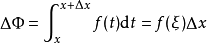








推導二





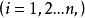








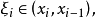


定理推廣
二重積分形式





曲線積分形式


 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫




發展簡史


微積分基本定理一般指本詞條














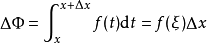













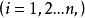








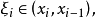









 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫





微積分基本定理描述了微積分的兩個主要運算──微分和積分之間的關係。定理的第一部分,稱為微積分第一基本定理,表明不定積分是微分的逆運算。這一部分定理的重要...
亨斯托克微積分基本定理(calculus fun-damental theorem for Henstock integrals)是黎曼積分和勒貝格積分的微積分基本定理在亨斯托克積分情形的推廣,若函式F<x)在壓,...
中文名 積分 外文名 integral 基本原理 微積分基本定理 提出者 艾薩克·牛頓 特點 發展的動力來自於實際套用中的 基本介紹 積分發展的動力源自實際套用中的...
分部積分法是微積分學中的一類重要的、基本的計算積分的方法。它是由微分的乘法法則和微積分基本定理推導而來的。它的主要原理是將不易直接求結果的積分形式,轉化...
微積分基本定理由艾薩克·牛頓和戈特弗里德·威廉·萊布尼茨在十七世紀分別獨自確立。微積分基本定理將微分和積分聯繫在一起,這樣,通過找出一個函式的原函式,就可以...
《 直來直去的微積分》是 2010年 科學出版社出版社出版的圖書,作者是 張景中。...... 定義了函式的導數,證明了導數的常用性質;定義了定積分,推出了微積分基本...
3.5.2定積分的概念3.5.3定積分的幾何意義3.5.4定積分的性質習題3 53.6微積分基本公式3.6.1變上限的定積分3.6.2微積分基本定理習題3 6...
5.1定積分的概念與性質5.1.1定積分實際問題舉例5.1.2定積分的定義5.1.3定積分的幾何意義5.1.4定積分的性質習題5.15.2微積分基本定理...
微積分學,數學中的基礎分支。內容主要包括函式、極限、微分學、積分學及其套用。函式是微積分研究的基本對象,極限是微積分的基本概念,微分和積分是特定過程特定形式...
換元積分法(Integration By Substitution)是求積分的一種方法,主要通過引進中間變數作變數替換使原式簡易,從而來求較複雜的不定積分。它是由鏈式法則和微積分基本...
在微積分中,一個函式f 的不定積分,或原函式,或反導數,是一個導數等於f 的函式 F ,即F′ = f。不定積分和定積分間的關係由微積分基本定理確定。其中F是f...
該定理的一個直接推論,是在單連通域內全純函式的路徑積分可以用類似於微積分基本定理的方法來計算:設 是複平面的一個開子集。 是一個 上的全純函式。函式f在...
正因為這個理論,揭示了積分與黎曼積分本質的聯繫,可見其在微積分學以至更高等的數學上的重要地位,因此,牛頓-萊布尼茲公式也被稱作微積分基本定理。...
牛頓-萊布尼茲公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函式的原函式或者不定積分之間的聯繫。牛頓-萊布尼茨公式的內容是一個...
就在這個時候,牛頓和萊布尼茨將微分及積分兩個貌似不相關的問題,透過「微積分基本定理」或「牛頓-萊布尼茨公式」聯繫起來,說明求積分基本上是求微分之逆,求微分也是...
