基本介紹
- 中文名:牛頓-萊布尼茨公式
- 外文名:Newton-Leibniz formula
- 分類:數學
- 又名:微積分基本定理
- 時間:1677年
- 提出 :牛頓 萊布尼茨
定理定義
定義




弱化條件






公式推導
推導一




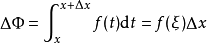








推導二





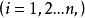








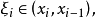


定理推廣
二重積分形式





曲線積分形式


 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫




發展簡史
















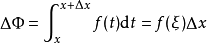













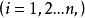








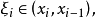









 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫





牛頓-萊布尼茲公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函式的原函式或者不定積分之間的聯繫。牛頓-萊布尼茨公式的內容是一個...
由於名稱相似,不少人將牛頓-萊布尼茨公式與萊布尼茨公式相混淆,事實上他們是兩個完全不同的公式。牛頓-萊布尼茨公式是微積分學中的一個重要公式,它把不定積分與定...
萊布尼茲公式,也稱為乘積法則,是數學中關於兩個函式的積的導數的一個計算法則。不同於牛頓-萊布尼茨公式,萊布尼茨公式用於對兩個函式的乘積求取其高階導數。萊布尼茨...
萊布尼茨公式給出了含參變數常義積分在積分符號下的求導法則。萊布尼茨是德國自然...在數學上,與牛頓並稱為微積分的創始人,改進了帕斯卡的加法器,設計並製造了一...
積分的定義迥然不同,定積分是求圖形的面積,即是求微元元素的累加和,而不定積分則是求其原函式,而牛頓和萊布尼茨則使兩者產生了緊密的聯繫(詳見牛頓-萊布尼茨公式...
積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),而不定積分是一個函式表達式,它們僅僅在數學上有一個計算關係(牛頓-萊布尼茨公式),其它一...
根據牛頓-萊布尼茨公式,許多函式的定積分的計算就可以簡便地通過求不定積分來進行。這裡要注意不定積分與定積分之間的關係:定積分是一個數,而不定積分是一個表達式...
並通過後來以他們的名字命名的著名公式— [1] 牛頓-萊布尼茨公式—反映了這種互逆關係,從而使本來各自獨立發展的微分學和積分學結合而成一門新的學科—微積分學。...
柯西簡潔而嚴格地證明了微積分學基本定理即牛頓-萊布尼茨公式。他利用定積分嚴格證明了帶餘項的泰勒公式,還用微分與積分中值定理表示曲邊梯形的面積,推導了平面曲線...
定積分,牛頓-萊布尼茨公式立體幾何:祖暅原理長方形性質定理詞條標籤: 科學, 學科 圖集 幾何定理圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:44次歷史版本...
定理的第二部分,稱為微積分第二基本定理或“牛頓-萊布尼茨公式”,表明定積分可以用無窮多個原函式的任意一個來計算。這一部分有很多實際套用,這是因為它大大簡化...
3牛頓-萊布尼茨公式 4分部積分法 5積分換元法 6有理函式的積分 7曲線的弧長 8數值積分 9反常積分 10面積的計算 11旋轉體的計算 12可分離變數的微分方程 第四...
4.理解積分上限的函式,會求它的導數,掌握牛頓-萊布尼茨公式.5.了解反常積分的概念,會計算反常積分.6.掌握用定積分表達和計算一些幾何量與物理量(平面圖形的面積、...
就在這個時候,牛頓和萊布尼茨將微分及積分兩個貌似不相關的問題,透過「微積分基本定理」或「牛頓-萊布尼茨公式」聯繫起來,說明求積分基本上是求微分之逆,求微分也是...
8.4 一橋飛架南北,天塹變通途——牛頓一萊布尼茨公式8.5 千樹萬樹梨花開——積分學的套用第9章 微分搭台方程唱戲9.1 開創“方程”的新局面——初識微分方程...
