基本介紹
- 中文名:分部積分法
- 外文名:Integration by parts
- 原理:乘積函式求微分法則的逆用
- 基本函式:五類基本函式
- 科目:高等數學
- 數學分支:數學分析原理
- 套用學科:數學
公式推導

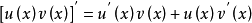






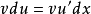
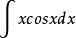



四種典型模式










模式一










模式二






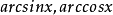





模式三






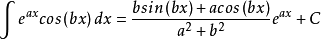




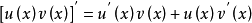






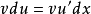
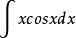





























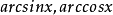











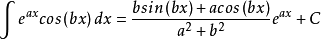


分部積分法是微積分學中的一類重要的、基本的計算積分的方法。它是由微分的乘法法則和微積分基本定理推導而來的。它的主要原理是將不易直接求結果的積分形式,轉化...
積分法 integral method; 是通過磁異常的積分運算求得磁性體產狀的定量解釋推斷方法。通過這種運算可以直接或間接的求得磁性體的產狀。積分法一般利用磁異常曲線的一...
在微積分中,一個函式f 的不定積分,或原函式,或反導數,是一個導數等於f 的...分部積分法的實質是:將所求積分化為兩個積分之差,積分容易者先積分。實際上是...
定積分分部積分法 設u=u(x),v=v(x)均在區間[a,b]上可導,且u′,v′∈R([a,b]),則有分部積分公式: [3] 定積分分點問題 編輯 ...
5.1 不定積分的概念5.2 不定積分的性質和基本積分公式5.3 直接積分法5.4 換元積分法5.5 分部積分法第6章 定積分6.1 定積分的概念...
分部積分法:設函式u=u(x)及v=v(x)具有連續導數,則其乘積的導數為:,移項得:對兩邊求不定積分,得:也可寫為:如果求 有困難,而求 比較容易時,分部積分公式...
以後凡是看到以上形式的積分,不需要繼續嘗試使用換元積分法或分部積分法等基本的積分技巧並且使用牛頓-萊布尼茨公式,因為以上積分都已經被證明了為非初等函式積分。...
7.4定積分的換元積分法與分部積分法習題7.47.5定積分的幾何套用習題7.57.6定積分的物理套用習題7.67.7反常積分習題7.7第7章補充題...
有理函式積分法是按一定步驟求有理函式不定積分的方法,求有理函式的積分時,先將有理式分解為多項式與部分分式之和,再對所得到的分解式逐項積分。有理函式的原...
。向量值R-S積分有許多類似於數值函式的R-S積分的性質。特別,有分部積分公式:如果 , 中有一個存在,則另一個必存在,且 。下面幾種向量值積分都屬於勒貝格型的...
7.1 積分的思想與方法7.1.1 定積分的概念7.1.2 定積分的性質7.2 牛頓-萊布尼茨公式7.2.1 定積分的換元積分法7.2.2 定積分的分部積分法...
1 不定積分的概念2 換元積分法3 分部積分法4 有理函式積分法5 無理函式積分法6 三角函式積分法習題6第七章 定積分1 定積分的概念...
第二積分法 分部積分法 混循環小數 第一積分法 同類二次根偏微分方程數學名詞六字及以上 一元一次方程 一元二次方程 完全平方公式 最簡二次根式...
9.2不定積分的換元法和分部積分法 9.3定積分 9.4可積函式類R[a,b] 9.5定積分性質 9.6廣義積分 9.7定積分與廣義積分的計算 9.8若干初等可積函式類 第十...
用分部積分法令由 的單調性推知即為變形後得到由求極限的夾逼準則,得到即為Wallis公式。 [2] Wallis公式公式的變形 編輯 Wallis公式還有一些變形:...
例如採用分部積分法,兩邊減掉 ,將得到0=1的結論。於是數學家們想到了利用積分變限函式來給出 的原函式,即定義一個新的函式根據這個定義立刻可以知道 。並且根據...
