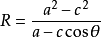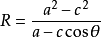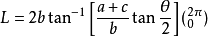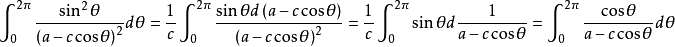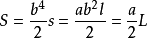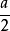極坐標定積分是以R為半徑,θ為積分變元,計算曲線周長的、面積的積分。
曲線的周長定積分為,曲線的面積定積分為。
設曲線ρ=R在區間[θ1,θ2]上非負連續,當dθ足夠小時,其角度對應的曲線長度為扇形曲線的長度,故曲線周長積分變數為Rdθ,當dθ足夠小時,曲線面積近似為直角三角形面積,等於一邊長度乘以高,故曲線面積積分變數為1/2R×Rdθ,由此得到曲線周長面積的定積分。
基本介紹
- 中文名:極坐標定積分
- 外文名:Polar coordinates definite integral
- 學科:數學
- 用處:計算曲線周長的、面積的積分
套用