在數學中,指數積分是函式的一種,它不能表示為初等函式,是特殊的不完全伽馬函式之一。
基本介紹
- 中文名:指數積分
- 外文名:Exponential Integral
- 所屬學科:數理科學
- 屬性:特殊的不完全伽馬函式
指數積分的定義





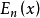

一階指數積分




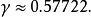
三階指數積分


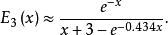

正弦積分函式與餘弦積分函式



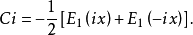



指數積分與其它函式的關係






在數學中,指數積分是函式的一種,它不能表示為初等函式,是特殊的不完全伽馬函式之一。





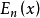







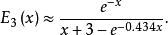




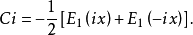








在數學中,指數積分是函式的一種,它不能表示為初等函式,是特殊的不完全伽馬函式之一。...
積分是微分的逆運算,即知道了函式的導函式,反求原函式。在套用上,積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊三角形的面積,這巧妙的求解方法是積分...
對數積分li(x)是一個特殊函式。它出現在物理學的問題中,在數論中也有重要性,主要出現在與素數定理與黎曼猜想的相關理論之中。...
三角積分是含有三角函式的一種積分。一些簡單的含有三角函式的積分,可在三角函式積分表中找到。三角積分是一種非初等函式。...
指數是冪運算aⁿ(a≠0)中的一個參數,a為底數,n為指數,指數位於底數的右上角,冪運算表示指數個底數相乘。當n是一個正整數,aⁿ表示n個a連乘。當n=0時,...
Windows 體驗指數測量計算機硬體和軟體配置的功能,並將此測量結果表示為稱作基礎分數的一個數字。較高的基礎分數通常表示計算機比具有較低基礎分數的計算機運行得更好...
用集成運算放大器OP07和三極體8050構成對數放大電路和反對數放大電路。利用PN節的指數伏安特性實現對數反對數運算,同時用三極體代替PN節以增加集電極電流動態運用範圍。...
指數插值(exponential interpolation)是常用的插值方法之一,指用指數函式之和作為插值函式的插值方法。例如,在分析放射性元素衰減時常被採用。...
赫斯特指數(英語:Hurst exponent)以英國水文學家哈羅德·赫斯特命名,起初被用來分析水庫與河流之間的進出流量,後來被廣泛用於各行各業的分形分析。...
假定在無限的環境中,種群增長是無限的,不受資源,空間等條件的限制;種群就發揮其內稟增長能力,種群增長呈指數式增長格局,這種增長規律,稱種群的指數式增長。可分為...
指數賦值(exponential valuation)是非阿基米德賦值的又一記法。設a是域F的非阿基米德賦值,對F中的a,若二(Cad = loga},則映射二:F'-> RU{二}稱為域F的一個...
B積分是在非線性光學中對於光非線性相位移的量測,是計算雷射光束中最不穩定空間頻率的指數成長程度,在數值上等效於延著雷射系統光軸的非線性相位移。...
工業生產指數(Industrial Production),縮寫為IIP,就是用加權算術平均數編制的工業產品實物量指數,是西方國家普遍用來計算和反映工業發展速度的指標,也是景氣分析的首選...
CT劑量指數是對一個單次軸向掃描產生的沿著體層平面垂直線劑量分布從-50mm到正+50mm的積分。...
復指數信號是指數信號的指數因子是複數時,稱之為復指數信號。復指數信號在物理上是不可實現的,但是它概括了多種情況。利用復指數信號可以表示常見的普通信號,如...
零點收斂指數(exponent of convergence of zeros)是量度函式零點稠密程度的一個量。...
B積分量測法是在非線性光學中對於光非線性相位移的量測,是計算雷射光束中最不穩定空間頻率的指數成長程度,在數值上等效於延著雷射系統光軸的非線性相位移。...
崗位績效指數化法是指對考評對象的工作業績和所確定的崗位指數之間進行比較的考評方式。由於崗位指數是職位要素、崗位目標以及影響目標達成的各種因素的綜合指數,崗位...
基尼指數通常把0.4作為收入分配差距的“警戒線”,根據黃金分割律,其準確值應為0.382。一般已開發國家的基尼指數在0.24到0.36之間,美國偏高,為0.45 [4] 。中國...
