復指數信號是指數信號的指數因子是複數時，稱之為復指數信號。復指數信號在物理上是不可實現的，但是它概括了多種情況。利用復指數信號可以表示常見的普通信號，如直流信號、指數信號、正弦信號等。復指數信號的微分和積分仍然是復指數信號，利用復指數信號可以使許多運算和分析簡化。因此，復指數信號是信號分析中非常重要的基本信號。
基本介紹
- 中文名：復指數信號
- 套用：信號處理
復指數信號,相關介紹,直流信號,正弦信號,指數信號,正弦信號,抽樣信號,
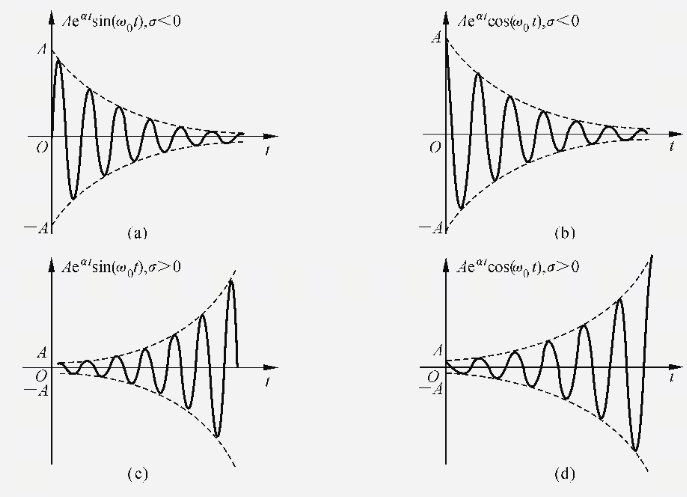
復指數信號
當指數信號的指數因子是複數時，稱之為復指數信號，其數學表達式為：
（1）若 >0，復指數信號的實部、虛部為增幅正弦信號；
（2）若 <0，復指數信號的實部、虛部為衰減正弦信號；
指數因子的虛部
則表示正弦與餘弦信號的角頻率，特殊情況是：
（1）當 =0，即s為虛數，則原公式可寫成虛指數信號形式，即為等幅正弦信號。虛指數信號的一個重要特性是具有周期性，其周期為2π/ω；
（2）當 =0，即s為實數，則復指數信號成為一般的指數信號；
（3）若 =0且 =0，即s=0，則復指數信號的實部和虛部都與時間無關，成為直流信號。
雖然實際上不能產生復指數信號，但是它概括了多種情況，可以利用復指數信號來描述各種基本信號，如直流信號、指數信號、正弦或餘弦信號以及增長或衰減的正弦與餘弦信號。復指數信號的微分和積分仍然是復指數信號，利用復指數信號可使許多運算和分析得以簡化。在信號分析理論中，復指數信號是一種非常重要的基本信號。
復指數信號：e^(jwt)，根據歐拉公式e^(jwt)=cos(wt)+jsin(wt)。於是|e^jwt|=cos^2(wt)+sin^2(wt)=1，即一個周期復指數信號e^jwt的絕對值的平方等於1。如果把這個函式作為控制系統的輸入函式，那么一想便知系統的輸出也應當是一個複數：根據複數相等實部實部相等、虛部虛部相等的原則，那么輸出的實部與輸入的實部：cos（wt）相對應；輸出的虛部與輸入的虛部：sin(wt)相對應。這有一個好處：輸入一個復指數函式就同時解決了系統輸出的振幅和相位的問題：因為輸出的振幅等於回響實部的平方與虛部的平方和的開方；而輸出的相位等於回響虛部與實部的比值的反正切。對於線性控制系統輸入是正弦的輸出也是正弦的，且周期不變。
相關介紹
直流信號
直流信號的數學表達式為f(t)=A其中，A為實數，其定義域為（－∞，+∞），若A=1，則稱之為單位直流信號。
正弦信號
正弦信號的數學表達式為f(t)=Acos(ωt+φ)其中，A、ω、φ分別稱為正弦信號的振幅、角頻率、初相位，且均為實數。其定義域為（－∞，+∞）。正弦信號具有如下性質：
（1）正弦信號是無時限信號。
（2）正弦信號是周期信號，其周期T=2π/ω。
（3）正弦信號的微分仍然是正弦信號。
（4）正弦信號滿足如下形式的二階微分方程，即
指數信號
指數信號的數學表達式為
其中，A和α是實數，其定義域為（－∞，+∞），係數A是t=0時指數信號的初始值，當A
為正實數時，若α>0,則指數信號的幅度隨時間增長而增大；若α<0，則指數信號的幅度
隨時間增長而衰減；在α=0的特殊情況下，信號不隨時間變化而變化，而成為直流信號。
正弦信號
正弦信號是指具有下列表達式形式的一類信號的總稱，即
其中，A為振幅；ω是角頻率；θ稱為初始相位，這三個參數稱為正弦信號的三要素。正弦信號是周期信號，其周期T與角頻率ω和頻率f滿足下列關係：
抽樣信號
抽樣信號用符號Sa(t)表示，公式：
抽樣信號具有如下性質；
（1）它是一個偶函式；
（2）當t=kπ，k是非零整數時，函式值等於零；
（3）Sa(t)曲線下的面積為π，即
（4）在t=0時存在一個重要的極限，即
與Sa(t)信號類似的是sin(t)信號，它的定義是
可以看出，Sa(t)信號與sinc(t)信號沒有本質的區別，它們只是在時間尺度上有所不同，所以有些書籍將這兩種符號通用。
抽樣信號是理想低通濾波器的單位衝激回響波形。在從連續信號抽樣變為離散信號過程中，可以認為信號是以抽樣信號Sa(t)為基本信號的一種分解。
