基本介紹
積分表示法


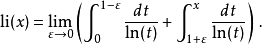
歐拉對數積分
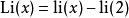
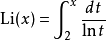

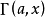
級數表示法



漸近展開式

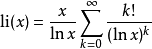

數論中重要性

不定積分





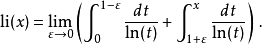
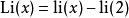
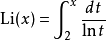

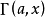




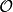
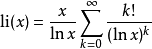




對數積分li(x)是一個特殊函式。它出現在物理學的問題中,在數論中也有重要性,主要出現在與素數定理與黎曼猜想的相關理論之中。...
積分表是在積分計算中為了使用與方便,把常用的積分公式匯集成的一種數學用表。積分表是按照被積函式的類型來排列的。求積分時,可根據被積函式的類型直接地或經過...
在數學中,指數積分是函式的一種,它不能表示為初等函式,是特殊的不完全伽馬函式之一。...
積分是微分的逆運算,即知道了函式的導函式,反求原函式。在套用上,積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊三角形的面積,這巧妙的求解方法是積分...
在數學中,對數是對求冪的逆運算,正如除法是乘法的倒數,反之亦然。 這意味著一個數字的對數是必須產生另一個固定數字(基數)的指數。 在簡單的情況下,乘數中的...
對數求導法是一種求函式導數的方法。取對數的運算可將冪函式、指數函式及冪指函式運算降格成為乘法運算,可將乘法運算或除法運算降格為加法或減法運算,使求導運算計算...
對數方程(logarithmic equation)一種超越方程,指含有關於未知數的對數式,而不含其他超越式的方程。即在對數符號後面含有未知數的方程,叫做對數方程。...
三角積分是含有三角函式的一種積分。一些簡單的含有三角函式的積分,可在三角函式積分表中找到。三角積分是一種非初等函式。...
對數函式lg,是以10為底的對數(常用對數),如lg 10=1。lg即為log10...... 對數函式lg,是以10為底的對數(常用對數),如lg 10=1。 lg即為log10 [1] ...
分部積分法是微積分學中的一類重要的、基本的計算積分的方法。它是由微分的乘法法則和微積分基本定理推導而來的。它的主要原理是將不易直接求結果的積分形式,轉化...
對數容量(logarithmic capacity)是由對數核確定的一種容量。在R中,關於對數核考慮緊集F的倒容量Wl(F),當限制F包含於單位圓B內時,若Wl(F)>0,則把1/Wl(F)...
對數平均溫差,兩種流體在熱交換器中傳熱過程溫差的積分的平均值。...... 對數平均溫差,兩種流體在熱交換器中傳熱過程溫差的積分的平均值。中文名 對數平均溫差 外...
對數坐標圖又稱為伯德曲線或伯德圖(bode plot或bode diagram)。它由兩幅圖組成:一幅是對數幅頻特性圖(magnitude plot),它的縱坐標為20lg|G(jω)|,單位是...
對數是中學初等數學中的重要內容,蘇格蘭數學家納皮爾首創“對數”這種高級運算。對數,可以縮短計算時間,“在實效上等於把天文學家的壽命延長了許多倍...
最簡對數方程是一種特殊的對數方程,指未知數指數為1的對數方程。形如logax=b(a>0,a≠1)的方程稱為最簡對數方程。根據對數的定義,原方程轉換為指數式x=ab,...
