基本介紹
- 中文名:柯西主值
- 外文名:Cauchy principal value
- 適用範圍:數理科學
定義

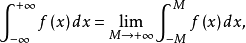



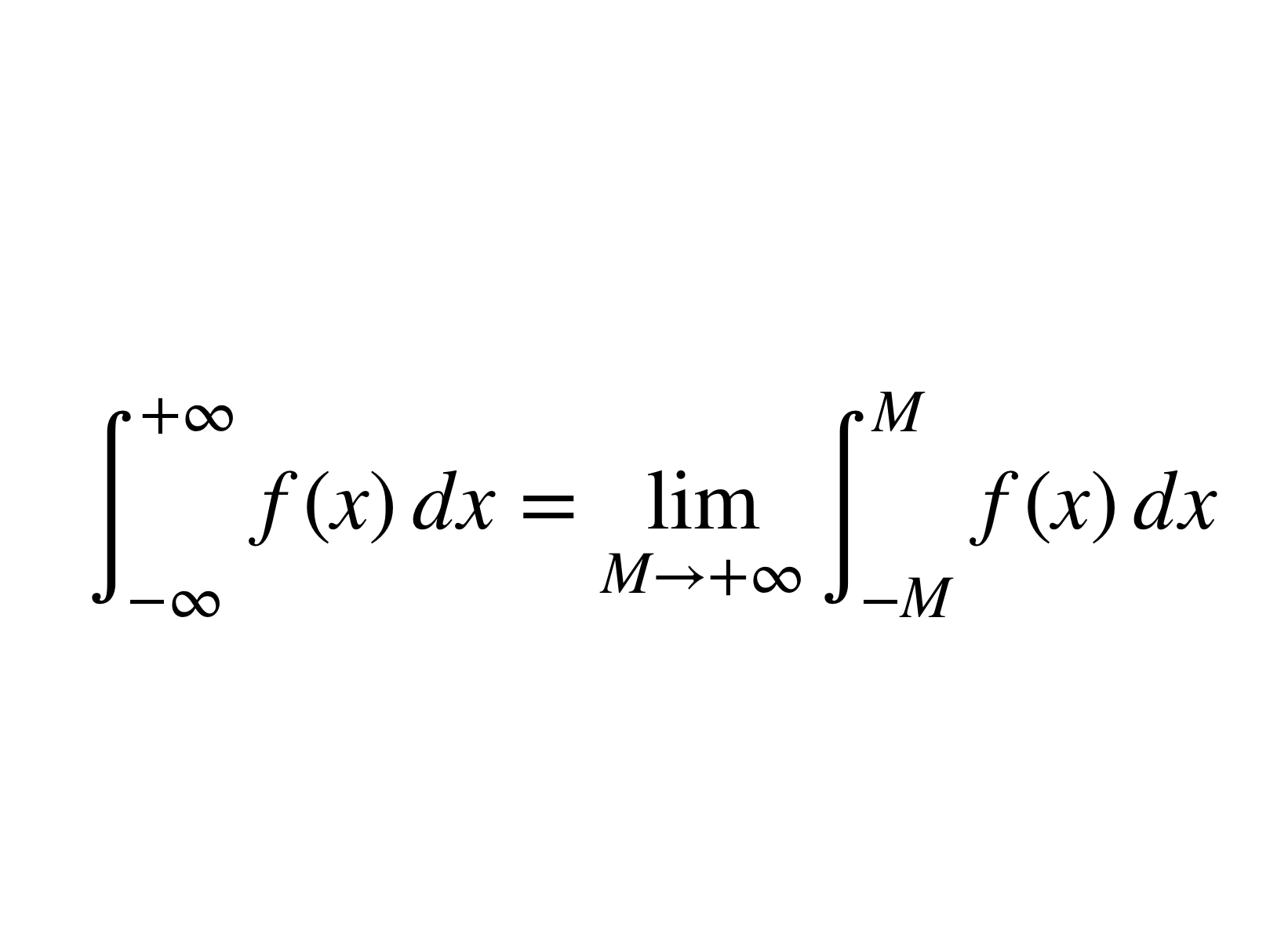

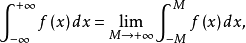



柯西主值是在微積分中,實數線上的某類瑕積分,為紀念柯西而得此名。...... 柯西主值是在微積分中,實數線上的某類瑕積分,為紀念柯西而得此名。...
柯西主值積分是以特殊方式定義的反常積分,其值又稱為相應積分的柯西主值。...... 柯西主值積分是以特殊方式定義的反常積分,其值又稱為相應積分的柯西主值。...
柯西型積分柯西型積分的主值 編輯 在L為簡單光滑閉曲線的情形下,進一步研究柯西積分的性質,為了簡單起見,將L所圍成的有界區域記作D+(不妨設原點在其內部),以...
柯西奇異積分方程(Cauehy singular integral equations)是一類最基本且具有廣泛實際套用的奇異積分方程,其積分是柯西主值意義下的。柯西奇異積分方程與弗雷德霍姆積分...
柯西核的奇異積分方程的特點是未知函式出現在發散的積分號下,該積分只在柯西主值下有意義,以及和它的特徵方程有密切聯繫的黎曼問題。...
都有定義: [1] 在這裡,ln表示自然對數。函式1/ln (t)在t= 1處有一個奇點,當x> 1時,這個積分只能用柯西主值的概念來解釋:對數積分歐拉對數積分 編輯 由於...
柯西主值積分 相似詞 渦環目錄 1 定義 2 帶周期性邊界 面渦定義 編輯 為滿足流體壁面無滑移條件,在壁面上產生一個切向速度的間斷面(面渦),使流體通過面渦...
這個積分不是收斂的勒貝格積分,應當理解為柯西主值。這個公式要求c> 0,c>σ 和實數x> 0,但除以上條件以外別無限制。佩龍公式證明 編輯 ...
五、反常積分的柯西主值 習題6—5 綜合題六 第七章定積分的套用舉例 第八章常微分方程 附錄積分表參考資料 1. 大學數學系列教材(第三版)大學數學1 ....
表示柯西主值。 [1] 因此可析函式的實部和虛部並不獨立:函式的一部分可以重建整個函式 [2] 。克拉莫-克若尼關係式推導 編輯 推導克喇末-克勒尼希關係式是留數...
由於h(t)是不可積的,定義卷積的積分不收斂。因而希爾伯特變換是使用柯西主值(這裡記為p。v。)定義的。準確說來,函式(或信號)u(t)的希爾伯特變換是:...
在數學與信號處理的領域中,一個實值函式的希爾伯特變換(Hilbert transform)——...並考慮此積分為柯西主值(Cauchy principal value),其避免掉在τ=t以及τ=±∞...
常見的奇異積分方程有兩種:一種是核具有主值意義的奇性,例如柯西核;一種是積分區域為無窮的積分方程,例如維納-霍普夫方程。 前一種奇異積分方程的理論是在弗雷德...
,即對於一個支撐集包括0的測試函式而言,這個分布的作用效果不能表示為某個函式的作用。當然這個分布可以表示為一個柯西主值意義下的瑕積分。對於...
普萊姆利公式是柯西型積分的邊界值公式,在蘇聯的書刊中常被稱為索霍茨基公式。...... 普萊姆利公式是柯西型積分的邊界值公式,在蘇聯的書刊中常被稱為索霍茨基公...
1.3 Cauchy主值積分和Hadamard有限部分積分的概念1.4 彈性力學問題的位移邊界積分方程1.5 含裂紋彈性體位移邊界積分方程的不適定性1.6 彈性力學問題的面力邊界積分...
普萊姆利一索霍茨基公式是柯西型積分邊界值的基本公式。...... 其中右端的積分理解為柯西主值.公式(1)稱為普萊姆利一索霍茨基公式,此公式在研究柯西核奇異積分 ...
2.4 Cauchy主值積分的直接計算法2.5 超奇異積分的有限部分積分3 線性代數方程組的求解4 裂紋問題對偶邊界元法4.1 裂紋面的分元離散...
,其中,F是未知函式,B和f是給定函式,B(t)=cb(t),f(t)=vω(t),廣義積分理解為柯西主值的意義。在方程中出現的量的物理意義如下:2a是機翼的翼展,它假定...
積分 (8)作為勒貝格積分一般是發散的;注意到Ωj(y)在R的單位球面S上的積分為0,可以證明,積分(8)在柯西主值意義下存在,並且作為x的函式是連續的,從而u(x)...
作為嘗試,本書增添了高階奇異積分和推廣留數定理等具有實用價值的新內容;對教學難點的多值函式作了全新的處理;對柯西定理(同倫形式)、輻角原理、共形映照和解析...
4.關於邊界元方法中柯西主值積分的探討5.受有集中力的樣條邊界元法6.奇性校正特解場法計算任意點應力和位移7.全特解場邊界元方法...
