柯西型積分(integral of Cauchy type)是原本適用於解析函式的柯西積分表達式在連續函式情形的一種推廣。 在複變函數理論中,柯西型積分具有重要的地位,它是柯西積分的推廣,柯西積分是柯西型積分的特殊情況。
基本介紹
- 中文名:柯西型積分
- 外文名:integral of Cauchy type
- 所屬領域:複變函數論
- 相關概念:柯西積分、光滑曲線、連續函式等
基本介紹
定義

定理




柯西型積分的主值




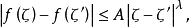






柯西型積分的極限值




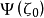







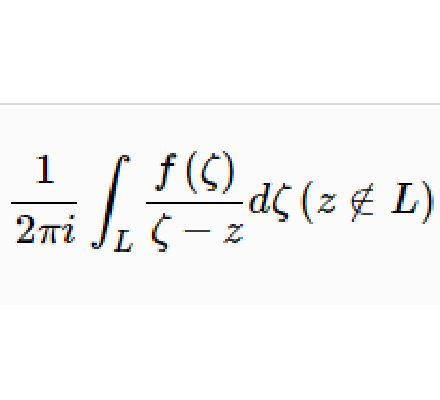
柯西型積分(integral of Cauchy type)是原本適用於解析函式的柯西積分表達式在連續函式情形的一種推廣。 在複變函數理論中,柯西型積分具有重要的地位,它是柯西積分的推廣,柯西積分是柯西型積分的特殊情況。









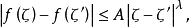










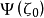







柯西型積分(integral of Cauchy type)是原本適用於解析函式的柯西積分表達式在連續函式情形的一種推廣。 在複變函數理論中,柯西型積分具有重要的地位,它是柯西積分...
柯西-賽格積分表示是單複變函數論中柯西型積分的推廣。華羅庚引進並證明了在一般有界圓型星形域上,存在一類柯西積分公式,稱為柯西-賽格積分公式。...
勒雷積分表示公式是一種多複變函數論的柯西型積分,即所謂勒雷積分表示公式。...... 勒雷積分表示公式是一種多複變函數論的柯西型積分,即所謂勒雷積分表示公式。...
在柯西型積分的表達式中,f(t)稱為它的核密度,1/t-z稱為柯西核。柯西核的奇異積分方程包括希爾伯特核的奇異積分方程,這是研究得最早和最完整的一類方程。...
本書主要討論緊黎曼面上的柯西型積分及其它一些函式論問題。主要包括以下幾個方面:如何確定緊黎曼面上的擬距離函式和圓環域;構造圓環域的柯西型積分核的完整方法;...
微分中值定理逆問題及漸近性 5.3 積分型柯西中值定理逆問題及漸近性 本章小結第6章 積分中值定理的逆 6.1 積分中值定理的逆問題 6.2 積分中值定理的逆...
柯西把區域上處處可微的複函數稱為單演函式,後人又把它們稱為全純函式、解析函式。B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分...
3.柯西不等式與劉維爾(Liouville)定理4.摩勒拉(Morera)定理5.柯西型積分§4.解析函式與調和函式的關係§5.平面向量場——解析函式的套用(一)...
