基本介紹
- 中文名:瑕積分
- 外文名: improper integral
- 領域:數學
- 相關:反常積分;廣義積分
定義
瑕點
定義1
定義2
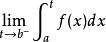
定義3
定理和性質
定理
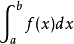

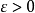
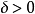
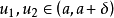
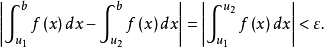
性質1
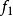
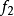
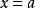
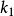
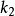
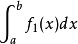
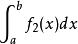
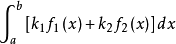
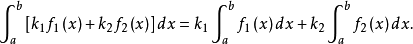
性質2
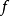
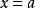
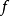
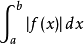
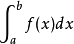
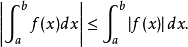
性質3
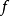
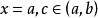
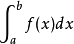
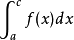
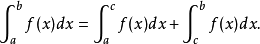
收斂判別法
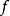
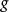
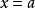

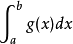
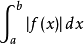
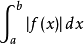
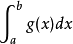
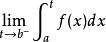
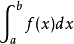

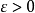
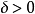
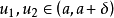
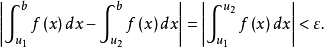
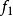
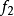
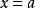
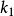
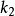
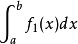
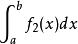
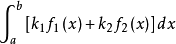
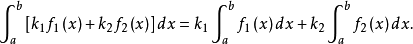
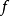
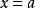
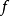
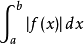
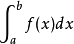
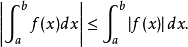
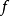
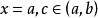
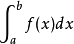
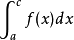
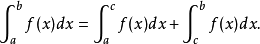
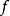
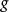
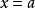

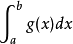
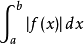
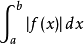
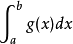
瑕積分 (improper integral)是高等數學中微積分的一種,是被積函式帶有瑕點的廣義積分。...
柯西型積分(integral of Cauchy type)是原本適用於解析函式的柯西積分表達式在連續函式情形的一種推廣。 在複變函數理論中,柯西型積分具有重要的地位,它是柯西積分...
定積分概念的推廣至積分區間無窮和被積函式在有限區間上為無界的情形稱為廣義積分,又名反常積分。其中前者稱為無窮限廣義積分,或稱無窮積分;後者稱為無界函式的廣義...
反常積分又叫廣義積分,是對普通定積分的推廣,指含有無窮上限/下限,或者被積函式含有瑕點的積分,前者稱為無窮限廣義積分,後者稱為瑕積分(又稱無界函式的反常積分)...
含參量積分(integral with parameters)是多元函式對其一部分自變數的積分。設f(x,y)為定義在矩形區域R=[a,b]×[c,d]上的二元函式,若對於[a,b]上每一固定...
狄利克雷(1805~1859) Dirichlet,Peter Gustav Lejeune 德國數學家。對數論、數學分析和數學物理有突出貢獻,是解析數論的創始人之一。狄利克雷(Dirichlet)積分,即 ...
《套用數學基礎(Ⅰ)——一元微積分》是2007年化學工業出版社出版的圖書,作者是高小明。...
廣義重積分(generalized multiple integral)是廣義黎曼重積分的簡稱,又稱反常重積分或非正常重積分,是一類多元函式積分,指無界多元函式及無界集上多元函式的積分。n重...
柯西主值是在微積分中,實數線上的某類瑕積分,為紀念柯西而得此名。...... 柯西主值是在微積分中,實數線上的某類瑕積分,為紀念柯西而得此名。...
反常積分分為兩種,一種是積分區間含有無窮大的反常積分(又叫做無窮限的反常積分),另一種是被積函式為無界函式的反常積分(又叫做無界函式的反常積分、瑕積分)。...
