反常積分又叫廣義積分,是對普通定積分的推廣,指含有無窮上限/下限,或者被積函式含有瑕點的積分,前者稱為無窮限廣義積分,後者稱為瑕積分(又稱無界函式的反常積分)。
基本介紹
- 中文名:反常積分
- 外文名:improper integral
- 別稱:廣義積分
- 特點:積分區間無窮
- 幾何意義:函式在一點的值無窮,但面積可求
- 學科:數學
簡述
幾何意義

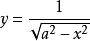
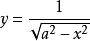
類型
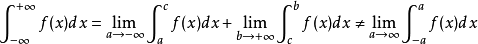
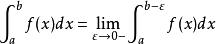


斂散性判斷
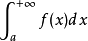


反常積分又叫廣義積分,是對普通定積分的推廣,指含有無窮上限/下限,或者被積函式含有瑕點的積分,前者稱為無窮限廣義積分,後者稱為瑕積分(又稱無界函式的反常積分)。

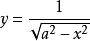
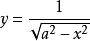
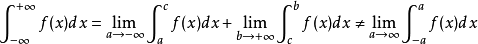
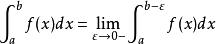


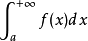

反常積分又叫廣義積分,是對普通定積分的推廣,指含有無窮上限/下限,或者被積函式含有瑕點的積分,前者稱為無窮限廣義積分,後者稱為瑕積分(又稱無界函式的反常積分)...
定積分概念的推廣至積分區間無窮和被積函式在有限區間上為無界的情形成為廣義積分,又名反常積分。其中前者稱為無窮限廣義積分,或稱無窮積分;後者稱為無界函式的廣義...
瑕積分 (improper integral)是高等數學中微積分的一種,是被積函式帶有瑕點的廣義積分。...
積分變換無論在數學理論或其套用中都是一種非常有用的工具。最重要的積分變換有傅立葉變換、拉普拉斯變換。由於不同套用的需要,還有其他一些積分變換,其中套用較為...
狄利克雷(1805~1859) Dirichlet,Peter Gustav Lejeune 德國數學家。對數論、數學分析和數學物理有突出貢獻,是解析數論的創始人之一。狄利克雷(Dirichlet)積分,即 ...
柯西主值積分是以特殊方式定義的反常積分,其值又稱為相應積分的柯西主值。...... 柯西主值積分是以特殊方式定義的反常積分,其值又稱為相應積分的柯西主值。...
黎曼積分(Riemann Integral),也就是所說的正常積分、定積分。在實分析中,由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上...
積分判別法(integral test)以廣義積分為工具,判別各項遞減的正項級數收斂性的一種判別法。...
積分學(integral calculus)數學分析的分支學科。即研究各種積分(理論、計算和套用)以及它們之間的關係的學科。積分學也是高等數學的基礎學科之一。積分學的研究對象...
Г函式是含參變數的以無窮乘積函式定義的反常積分。作為歐拉積分中一個重要的積分,它與B函式存在一定的聯繫。並且它在定積分也有重要的套用。...
主要用於判定數項級數的收斂、函式項級數的一致收斂、反常積分的收斂以及反常含參積分的一致收斂等。中文名 阿貝爾判別法 外文名 Abel Discriminance 提出者 ...
在機率統計和其他套用學科中會經常用到伽瑪函式和貝塔函式,有的反常積分的計算最後也會歸結為貝塔函式或伽瑪函式。貝塔函式又稱為 B 函式,需要注意這裡 B 是大寫...
反常積分分為兩種,一種是積分區間含有無窮大的反常積分(又叫做無窮限的反常積分),另一種是被積函式為無界函式的反常積分(又叫做無界函式的反常積分、瑕積分)。...
條件收斂是一種微積分上的概念。如果級數ΣUn收斂,而Σ∣Un∣發散,則稱級數ΣUn條件收斂。...
狄利克雷(Dirichlet)判別法是微積分中一條十分重要的判定法則,與阿貝爾(Abel)判別法合稱為A-D判別法。主要用於判定數項級數的收斂、函式項級數的一致收斂、反常...
魏爾斯特拉斯判別法(Weierstrass Discriminance)是分析學中一條十分重要的判定法則,主要用於判定數項級數的收斂、函式項級數的一致收斂、反常積分的收斂以及反常含參...
Dini定理 既可以指用來表示函式序列收斂的dini定理,也可以是含參變數的反常積分收斂的dini定理Dim...
