基本介紹
- 中文名:貝塔函式
- 外文名:Beta function
- 別名:Beta函式,B函式,第一歐拉積分
- 基本性質:P>0,Q>0時連續,對稱性
- 重要關係:與Γ(x)、不完全Beta函式的關係
- 套用學科:機率統計、數學分析
貝塔函式簡介

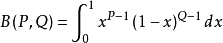
貝塔函式性質
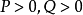

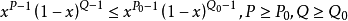

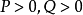


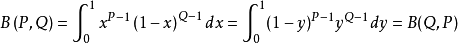




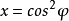


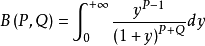




與其它函式


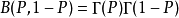

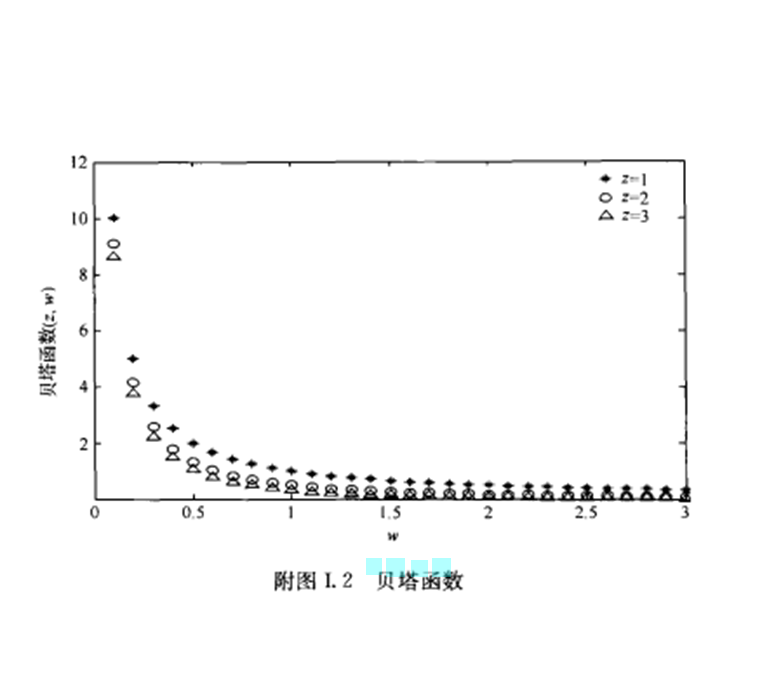

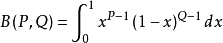
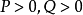

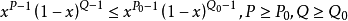

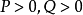


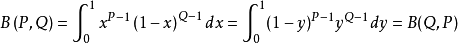




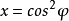


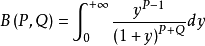






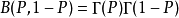

在機率統計和其他套用學科中會經常用到伽瑪函式和貝塔函式,有的反常積分的計算最後也會歸結為貝塔函式或伽瑪函式。貝塔函式又稱為 B 函式,需要注意這裡 B 是大寫...
貝塔分布(Beta Distribution) 是一個作為伯努利分布和二項式分布的共軛先驗分布的密度函式,在機器學習和數理統計學中有重要套用。在機率論中,貝塔分布,也稱Β分布,是...
不完全貝塔函式(incomplete beta function)機率函式的一種.當P>0且Q>0時收斂。...... 這個積分又稱為第一類歐拉積分,,很顯然當x取1時,結果就變成完全的貝塔函...
伽瑪函式(Gamma函式),也叫歐拉第二積分,是階乘函式在實數與複數上擴展的一類函式。該函式在分析學、機率論、偏微分方程和組合數學中有重要的套用。與之有密切聯繫...
分布參數A服從貝塔分們的復複合泊松分布。 ...... 分布參數A服從貝塔分們的復複合泊松分布。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月...
在機率論中,Β分布也稱貝塔分布,是指一組定義在 (0,1)區間的連續機率分布。...... Β分布的累積分布函式是:其中 是不完全Β函式, 是正則不完全貝塔函式。...
歐拉積分是由瑞士數學家萊昂哈德·歐拉(Leonhard Euler , 1707.4.15~1783.9.18)整理得出的兩類特殊的含參變數的積分。由歐拉積分所定義的函式分別稱為伽馬函式...
11.2.1 [算法100] 伽馬函式 43911.2.2 [算法101] 貝塔函式 44111.2.3 [算法102] 階乘 44211.2.4 【實例58】 伽馬函式和貝塔函式求值 443...
1.1.2 伽馬函式、貝塔函式及Digamma函式1.1.3 不完全伽馬函式及不完全貝塔函式1.2 機率相關知識介紹1.2 1特徵函式1.2.2 矩與矩母函式...
