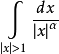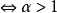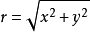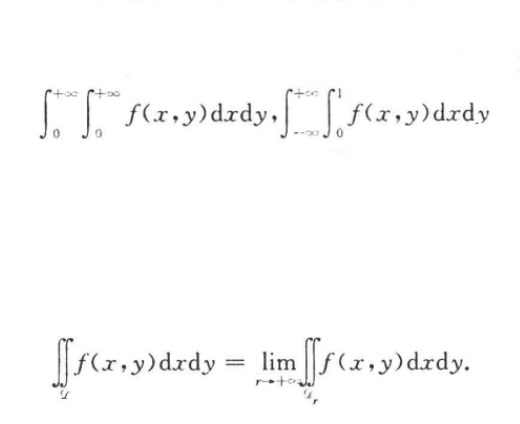廣義重積分(generalized multiple integral)是廣義黎曼重積分的簡稱，又稱反常重積分或非正常重積分，是一類多元函式積分，指無界多元函式及無界集上多元函式的積分。n重積分作為多變數的Riemann積分，要求積分域Ω是有界集，被積函式f：Ω→R為有界函式。然而，正如單變數函式的Riemann積分推廣到廣義積分(無窮積分與瑕積分)一樣，考察無界集上的重積分與無界函式的重積分，統稱為廣義(或反常)重積分。
基本介紹
- 中文名：廣義重積分
- 外文名：generalized multiple integral
- 別稱：廣義黎曼重積分，反常重積分
- 所屬學科：數學
- 簡介：一類多元函式積分
基本介紹,相關說明,
基本介紹
若積分區域D是個無界集，這時的重積分稱為廣義積分，譬如
相關說明
廣義重積分的兩點說明：
(1)Dr的取法中要求D—Dr與原點的距離隨r→+∞而趨於+∞；
(2)要求在一切不同Dr的取法下，有同一個極限，否則仍稱為發散或不可積。
但當f(x，y)≥o時，只要特別取一組Dr就夠了。
還有另一類型的廣義積分，這時積分區域D可能有界，但f(x，y)在D內某點
的任何鄰域無界(這時點稱為奇點)，或者在某條曲線上都是奇點(稱奇線)，這時也稱為廣義積分，其定義不外乎先去掉奇點(奇線)某個鄰域後先積分，再令該鄰域收縮到奇點(奇線)，若積分存在極限，則稱廣義積分存在或收斂或可積。
與一元廣義積分不同的是廣義重積分(重數≥2)可積必絕對可積(注意“絕對
可積”這句術語包含兩層意思：本身可積且也可積，將“絕對可積”誤解為僅僅絕對值積分收斂，這是錯誤的)。
對一重積分我們已知積分
收斂
(奇點x=0)；
收斂
(奇點x=±∞)。
對二重積分，則有(
)：
這用極坐標變換可證明，對類似的三重積分，只要將上面的“2”改為“3”，同樣，可類推到n重積分。
