絕對可積函式

絕對可積函式指絕對值可積的函式。對黎曼積分（包括重積分），可積函式必絕對可積，且函式的絕對值的積分不小於該函式的積分的絕對值。

基本介紹

• 中文名：絕對可積函式
• 外文名：absolutely integrable function
• 適用範圍：數理科學

簡介

絕對可積函式指絕對值可積的函式。

對黎曼積分（包括重積分），可積函式必絕對可積，且函式的絕對值的積分不小於該函式的積分的絕對值，即。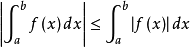

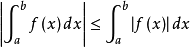
性質

在黎曼意義下絕對可積的函式不一定可積。例如，在有理點等於1在無理點等於-1的函式。

對一元函式的廣義積分，情形極不相同：|f(x)|廣義積分（即f(x)的廣義積分絕對收斂）時f廣義可積，反之不一定。

對於廣義重積分，通常採取這樣的方法定義：使絕對可積與可積等價，即廣義重積分收斂若且唯若它絕對收斂。

可積函式

數學上，可積函式是存在積分的函式。除非特別指明，一般積分是指勒貝格積分；否則，稱函式為"黎曼可積"（也即黎曼積分存在），或者"Henstock-Kurzweil可積"，等等。黎曼積分在套用領域取得了巨大的成功，但是黎曼積分的套用範圍因為其定義的局限而受到限制；勒貝格積分是在勒貝格測度理論的基礎上建立起來的，函式可以定義在更一般的點集上，更重要的是它提供了比黎曼積分更廣泛有效的收斂定理，因此，勒貝格積分的套用領域更加廣泛。