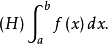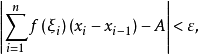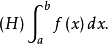絕對亨斯托克可積函式

絕對亨斯托克可積函式是一類特殊的(H)可積函式。

設f(x)是定義在[a,b]上的實值函式，若f(x)與|f(x)|在[a,b]上均(H)可積，則稱f(x)在[a,b]上絕對亨斯托克可積，簡稱絕對(H)可積。

基本介紹

• 中文名：絕對亨斯托克可積函式
• 外文名：absolute Henstock in-tegrable function
• 適用範圍：數理科學

定義

絕對亨斯托克可積函式是一類特殊的(H)可積函式。

設f(x)是定義在[a,b]上的實值函式，若f(x)與|f(x)|在[a,b]上均(H)可積，則稱f(x)在[a,b]上絕對亨斯托克可積，簡稱絕對(H)可積。

性質

若f(x)[a,b]上絕對(H)可積，則它在[a,b]上亦必(H)可積，其逆不真。

因為絕對(H)積分與(L)積分等價，所以它是具有黎曼形式的(L)積分，用這種黎曼形式來討論(L)積分，有利於同數學分析的銜接。

亨斯托克積分

亨斯托克積分是在20世紀50年代出現，後來發現它是與佩龍積分等價的一種積分。

設f(x)是定義在[a,b]上的實值函式，如果存在數A，對於任意ε>0，存在函式δ(ξ)>0，使得對每一分劃D:A=x₀<x₁<...<x_n=b和ξ₁,ξ₂,...,ξ_n，當ξ_i∈[x_i-1,x_i]⊂(ξ_i-δ(ξ_i),ξ_i+δ(ξ_i))(i=1,2,...,n)時有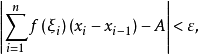

那么函式f(x)稱為亨斯托克意義可積，簡稱(H)可積。此時A稱為f(x)在[a,b]上的亨斯托克積分，記為