亨斯托克積分是在20世紀50年代出現,後來發現它是與佩龍積分等價的一種積分。1957年,亨斯托克給出的這種積分的定義是黎曼型的,它與佩龍積分等價,也與狹義當儒瓦積分等價,因而它給出了狹義當儒瓦積分的黎曼型定義,使狹義當儒瓦積分的處理簡化。
基本介紹
- 中文名:亨斯托克積分
- 外文名:Henstock integral
- 適用範圍:數理科學
簡介
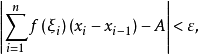
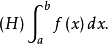
性質
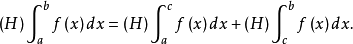



亨斯托克積分是在20世紀50年代出現,後來發現它是與佩龍積分等價的一種積分。1957年,亨斯托克給出的這種積分的定義是黎曼型的,它與佩龍積分等價,也與狹義當儒瓦積分等價,因而它給出了狹義當儒瓦積分的黎曼型定義,使狹義當儒瓦積分的處理簡化。
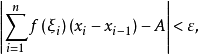
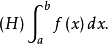
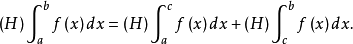



亨斯托克積分是在20世紀50年代出現,後來發現它是與佩龍積分等價的一種積分。1957年,亨斯托克給出的這種積分的定義是黎曼型的,它與佩龍積分等價,也與狹義當儒瓦積分...
亨斯托克微積分基本定理(calculus fun-damental theorem for Henstock integrals)是黎曼積分和勒貝格積分的微積分基本定理在亨斯托克積分情形的推廣,若函式F<x)在壓,...
絕對積分是使函式與其絕對值同時可積的那種積分,否則稱為非絕對積分。...... 當儒瓦積分、亨斯托克積分等也都是非絕對積分。參考資料 1. 《數學辭海》總編輯委員會...
亨斯托克控制收斂定理是亨斯托克積分在積分號下取極限的定理。若{f n(x)}是[a,b]上的(H)可積函式列,且在[a,b]上幾乎處處收斂於f(x)。...
囿變積分是與亨斯托克積分等價的一種積分。若F(x)為f(x)在[a,b]上的囿變原函式,這時稱f(x)在[a,b]上是囿變可積的,且囿變積分為F(b)-F(a)。...
因佩龍積分與狹義當儒瓦積分、亨斯托克積分等價,上述關係也就給出了狹義當儒瓦積分、亨斯托克積分與勒貝格積分的關係。 [1] 參考資料 1. 《數學辭海》總編輯委員會...
絕對亨斯托克可積函式是一類特殊的(H)可積函式。設f(x)是定義在[a,b]上的實值函式,若f(x)與|f(x)|在[a,b]上均(H)可積,則稱f(x)在[a,b]上...
馬克仙積分是與勒貝格積分等價的一種積分,是一個數學概念。此積分是由馬克仙(Mcshane , E. J.)引入的。馬克仙積分、絕對亨斯托克積分與勒貝格積分,這三種積分彼此...
囿變積分是與亨斯托克積分等價的一種積分。若F(x)為f(x)在[a,b]上的囿變原函式,這是稱f(x)在[a,b]上是囿變可積的,且囿變積分為F(b)-F(a)。 [...
