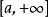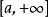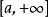絕對收斂一般用來描述無窮級數或無窮積分的收斂情況。如果級數ΣUn各項的絕對值所構成的級數Σ|Un|收斂,則稱級數ΣUn絕對收斂,級數ΣUn稱為絕對收斂級數。絕對收斂級數一定收斂。
若函式f(x)在[a,b]上可積,且|f(x)|的無窮積分(從a到+∞)上收斂,則稱 f(x) 的無窮積分(從a到+∞)絕對收斂。絕對收斂一定收斂。
基本介紹
- 中文名:絕對收斂
- 外文名:Absolute Convergence
- 歸屬學科:數學
- 描述:無窮級數或無窮積分的收斂情況
- 性質1:絕對收斂一定收斂
- 性質2:收斂不一定絕對收斂
級數
定義
定理





判別方法




















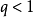





無窮積分
定義








定理



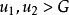



判定方法