基本介紹
定義
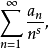
例子
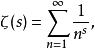
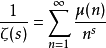
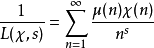
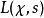
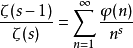
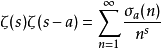
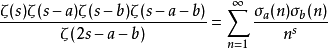
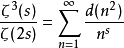
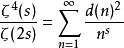
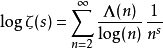
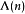
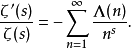
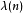
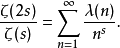
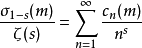
解析性質
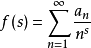
導數
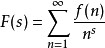
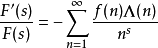
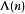
乘積
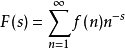
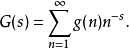
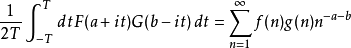
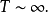
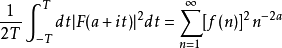

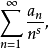
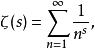
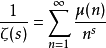
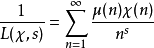
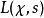
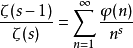
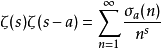
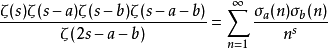
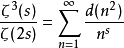
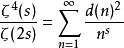
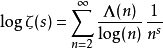
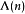
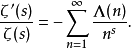
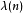
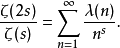
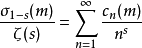
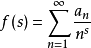
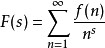
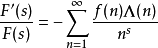
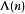
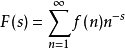
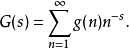
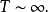
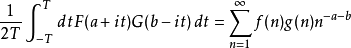
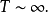
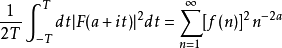
狄狄利克雷級數在解析數論中有重要的地位。黎曼ζ函式和狄利克雷L函式都可以用狄利克雷級數來定義。有猜測所有的狄利克雷級數組成塞爾伯格類函式都滿足廣義黎曼猜想。...
狄利克雷(Dirichlet)判別法是微積分中一條十分重要的判定法則,與阿貝爾(Abel)判別法合稱為A-D判別法。主要用於判定數項級數的收斂、函式項級數的一致收斂、反常...
在廣義狄利克雷級數的表達式中:若令a0=0,μ0=0,μn=log n(n=1,2,3,...),則得到狄利克雷級數。...
在數論中,狄利克雷定理說明對於任意互質的正整數a,d,有無限多個質數的形式如a+nd,其中n為正整數,即在等差數列a+d,a+2d,a+3d,...中有無限多個質數——...
狄利克雷函式(英語:dirichlet function)是一個定義在實數範圍上、值域不連續的函式。狄利克雷函式的圖像以Y軸為對稱軸,是一個偶函式,它處處不連續,處處極限不存在...
約翰·彼得·古斯塔夫·勒熱納·狄利克雷(Johann Peter Gustav Lejeune Dirichlet,勒熱納·狄利克雷是姓,1805年2月13日-1859年5月5日),德國數學家。他是解析數論...
狄利克雷L函式,又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式。...... 在數學中,狄利克雷L函式是狄利克雷級數的特例,它是形如下式的復變數函式在此χ 是一個...
約翰·彼得·古斯塔夫·勒熱納·狄利克雷(Johann Peter Gustav Lejeune Dirichlet),德國數學家。科隆大學博士。歷任柏林大學和格廷根大學教授。柏林科學院院士。是解析...
狄利克雷空間論(theory of Dirichlet space)是受BLD函式組成的希爾伯特空間論的啟發,在狄利克雷空間上建立的一種公理位勢論。...
比如x(t)的可微性或級數的一致收斂性。在閉區間上滿足狄利克雷條件的函式表示成的傅立葉級數都收斂。狄利克雷條件如下:在定義區間上,x(t)須絕對可積; 在...
2 絕對收斂級數及其性質 ▪ 定理2 ▪ 例1 3 阿貝爾判別法和狄利克雷判別法 ▪ 定理3(阿貝爾判別法) ▪ 定理4(狄利克雷判別法) 一般...
傅立葉級數的收斂性取決於函式有限數量的極大值和極小值,這就是通常稱為傅立葉級數的狄利克雷條件。參見傅立葉級數的收斂性之一。對於廣義函式或分布也可以用...
阿貝爾判別法(Abel Discriminance)是分析學中一條十分重要的判定法則,與狄利克雷判別法(Dirichlet Discriminance)合稱為A-D判別法。主要用於判定數項級數的收斂、...
由於和狄利克雷級數的關係,佩龍公式常被用於解析數論中的求和。例如我們對黎曼ζ函式有如下的著名積分表示:對於狄利克雷L函式也有類似的公式:...
之後的一次進展來自萊昂哈德·歐拉,他給出了調和級數呈對數發散。 [1] 除此...為了方便對數論函式作討論,此處引入狄利克雷卷積 : 。設 ,於是顯然 。於是,...
傅立葉級數的收斂性取決於函式有限數量的極大值和極小值,這就是通常稱為傅立葉級數的狄利克雷條件。參見傅立葉級數的收斂性之一。對於廣義函式或分布也可以用...
數論中,歐拉乘積公式(Euler product formula)是指狄利克雷級數可表示為一指標為素數的無窮乘積。這一乘積以瑞士數學家萊昂哈德·歐拉的名字命名,他證明了黎曼ζ函式...
7.初等函式的冪級數展開式.8.函式的傅立葉(Fourier)係數與傅立葉級數、狄利克雷(Dirichlei)定理、函式在[-l,l]上的傅立葉級數、函式在[0,l]上的正弦級數...
其後,P.G.L.狄利克雷套用分析方法於1837年解決了首項與公差互素的算術級數中有無限多個素數的問題,又於1839年推證出二次域的類數公式。他創立了研究數論的...
[1] 定義了代數數域上廣義的狄利克雷L級數做出了數域上狄利克雷素數定律的模擬。 [1] 將二次數域套用於模函式的構造理論,在橢圓模函式的研究上取得了新的進...
考慮狄利克雷級數解析延拓到s=0處的值,如果存在便是唯一的,將其定義為相應級數的和便給出了一個可和法。這個可和法有時會被混同於zeta函式的正則化。...
黎曼-西格爾公式,用於計算虛部為T點上黎曼ζ函式的值,使用約N=T1/2項的有限狄利克雷級數,所以要找到N個黎曼ζ函式的值時,它將加速約T1/2倍。這將找到虛部不...
這個定理有許多其他的形式和進一步的研究,並且在整函式的漸近值,解析數論和狄利克雷級數論的研究中有重要的套用。最大模定理施瓦茲引理 編輯 ...
是否收斂。下面將介紹5種判別級數是否收斂的方法。[1] (1)【阿貝爾判別法】若 為單調有界數列,且級數 收斂,則級數 收斂。(2)【狄利克雷判別法】若...
