默比烏斯函式,也稱為莫比烏斯函式、繆比烏斯函式,數論函式,由德國數學家和天文學家默比烏斯(August Ferdinand Möbius ,1790–1868)提出。梅滕斯(Mertens)首先使用μ(n)作為莫比烏斯函式的記號,故也被稱為梅滕斯函式。默比烏斯函式在數論中有著廣泛套用。
基本介紹
- 中文名:默比烏斯函式
- 外文名:Mo&4&bius function
- 領域:數理科學
- 別名:莫比烏斯函式;繆比烏斯函式
定義
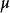
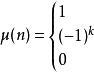 | 若 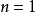 |
若  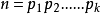 | |
若   |
 圖1.μ的首50個值
圖1.μ的首50個值性質
性質1


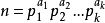
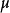
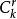
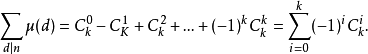
性質2
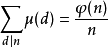
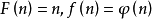
與其他函式的關係
1.梅滕斯函式

2.生成函式
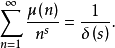
3.無窮級函式