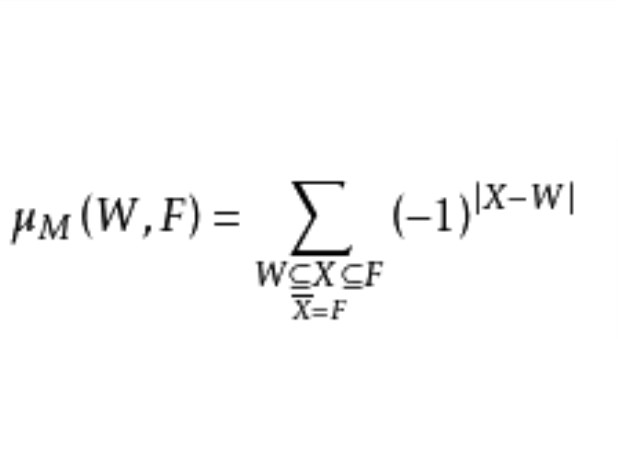默比烏斯不變數

默比烏斯不變數(Möbius invariant)是一種度量，指默比烏斯函式在擬陣M(E)上的不變數，記為μ(L)=μ_L(0，1)，這裡L為M的平集構成的格，0和1分別為L上的最小元和最大元，μ_L(x，y)為格L上的默比烏斯函式。

基本介紹

• 中文名：默比烏斯不變數
• 外文名：Möbius invariant
• 所屬學科：數學
• 所屬問題：離散數學（組合序）
• 簡介：默比烏斯函式在擬陣上的不變數

基本介紹

默比烏斯不變數指默比烏斯函式在擬陣M(E)上的不變數，記為μ(L)=μ_L(0，1)，這裡L為M的平集構成的格，0和1分別為L上的最小元和最大元，μ_L(x，y)為格L上的默比烏斯函式，對於L上的區間[u，v]，其上的默比烏斯不變數為μ_L(u，v)，這樣可以把偏序集上的默比烏斯函式擴充到擬陣M(E)上：當X，F均為L的元素時，取μ_M(X，F)=μ_L(X，F)；當F為L的元素，而X不是L的元素時，取μ_M(X，F)=0；當F不是L的元素時，μ_M(X，F)無定義；當F為L的元素，W為E的子集時，

其中，為X的閉包，對於均勻擬陣U_k，n，其默比烏斯不變數：

μ(U_k，n)=(-1)^r+1(0<k≤n).

而對於布爾代數B_n=U_n，n，μ(B_n)=(-1)ⁿ。

默比烏斯不變數的性質

擬陣上的默比烏斯不變數μ(M)具有類似於圖的不變數的如下性質：

1.當E的元素e不是擬陣的單點割集時，則

μ(M)=μ(M-e)-μ，

這裡M-e，M\e分別為關於e的刪除和收縮.

2.若M為M₁，M₂的直接和，即M=M₁⊕M₂，則μ(M)=μ(M₁)μ(M₂).

默比烏斯函式

默比烏斯函式(Möbius function)是一類結合函式，即從有限偏序集P=(E，≤)的笛卡兒積集P×P映到整數集Z上且滿足如下條件的映射μ：

1.若x≰y則μ(x，y)=0；

2.μ(x，z)=δ(x，y)，

這裡δ(x，y)的值僅當x=y時為1，其他均為0，條件1和2分別對應於x和y之間無接合關係及有接合關係，且條件2等價於μ(x，x)=1和

μ(x，y)=-μ(x，z).

因此，μ(x，y)的值可以從y=x出發，依次遞推地求出.這表明μ(x，y)僅與區間[x，y]有關，而與P的其他部分無關，特別地，當y覆蓋x時，μ(x，y)=-1，這樣偏序集P的結構可表現為函式μ(x，y)的簡潔數字值，條件2還可代之以其對稱形式：

μ(z，y)=δ(x，y).

對於P上的函式f和g，若g為f的和函式：

g(x)=f(y)，

則可藉助於μ而把f表示出來

f(x)=μ(x，y)f(y).

從形式上看，若把g對應於積分，則μ對應於積分逆公式中的導數，若μ*為P的對偶偏序集P*上的默比烏斯函式，則μ*(x，y)=μ(y，x)。此外，對於偏序集P和Q的笛卡兒積集P×Q上的默比烏斯函式，有μ_P×Q((x，y)，(u，v))=μ_P(x，u)μ_Q(y，v)。