發現歷史 發現
德金把它作為一種特殊的格。由於缺乏
物理 背景,所以研究緩慢,到了20世紀30~40年代才有了新的進展,大約在 1935年, M.H.斯通首先指出布爾代數與環之間有明確的聯繫,這使布爾代數在理論上有了一定的發展。布爾代數在代
數學 (
代數結構 )、
邏輯演算 、
集合論 、拓撲空間理論、測度論、
機率論 、泛函分析等數學分支中均有套用;1967年後,在數理邏輯的分支之一的公理化集合論以及
模型論 的理論研究中,也起著一定的作用。近幾十年來,布爾代數在自動化技術、電子計算機的邏輯設計等工程技術領域中有重要的套用。
布爾代數 數學家G.布爾 1835年,20歲的
喬治·布爾 開辦了一所私人授課學校。為了給學生們開設必要的數學課程,他興趣濃厚地讀起了當時一些介紹數學知識的教科書。不久,他就感到驚訝,這些東西就是數學嗎?實在令人難以置信。於是,這位只受過初步
數學訓練 的青年自學了艱深的《
天體力學 》和很抽象的《分析力學》。由於他對代數關係的對稱和美有很強的感覺,在孤獨的研究中,他首先發現了不變數,並把這一成果寫成論文發表。這篇高質量的論文發表後,布爾仍然留在國小教書,但是他開始和許多第一流的英國數學家交往或通信,其中有數學家、
邏輯學家 德·摩根 。
摩根 在19世紀前半葉捲入了一場著名的爭論,布爾知道摩根是對的,於是在1848年出版了一本薄薄的小冊子來為朋友辯護。這本書是他6年後更偉大的東西的預告,它一問世,立即激起了摩根的讚揚,肯定他開闢了新的、棘手的研究
科目 。布爾此時已經在研究
邏輯代數 ,即布爾代數。他把邏輯簡化成極為容易和簡單的一種代數。在這種代數中,適當的材料上的“
推理 ”,成了公式的初等運算的事情,這些公式比過去在中學代數第二年級課程中所運用的大多數公式要簡單得多。這樣,就使邏輯本身受數學的支配。為了使自己的研究工作趨於完善,布爾在此後6年的漫長時間裡,又付出了不同尋常的努力。1854年,他發表了《思維規律》這部傑作,當時他已39歲,布爾代數問世了,
數學史 上樹起了一座新的里程碑。幾乎像所有的新生事物一樣,布爾代數發明後沒有受到人們的重視。歐洲大陸著名的數學家蔑視地稱它為沒有數學意義的、
哲學 上稀奇古怪的東西,他們懷疑
英倫 島國的數學家能在數學上做出獨特貢獻。布爾在他的傑作出版後不久就去世了。20世紀初,
羅素 在《數學原理》中認為,“純數學是布爾在一部他稱之為《思維規律》的著作中發現的。”此說一出,立刻引起世人對布爾代數的注意。今天,布爾發明的邏輯代數已經發展成為純數學的一個主要分支。
德·摩根 在
離散數學 中,布爾代數(有時叫
布爾格 )是有補分配格(可參考格的定義)可以按各種方式去認為元素是什麼;最常見的是把它們當作一般化的真值。作為一個簡單的例子,假設有三個條件是獨立的為真或為假。布爾代數的元素可以接著精確指定那些為真;那么布爾代數自身將是所有八種可能性的一個蒐集,和與之在一起的組合它們的方式。
離散數學 有時也被稱為布爾代數的一個相關主題是
布爾邏輯 ,它可以被定義為是所有布爾代數所公有的東西。它由在布爾代數的元素間永遠成立的關係組成,而不管你具體的那個布爾代數。因為
邏輯門 和某些電子電路的代數在形式上也是這樣的,所以同在數理邏輯中一樣,布爾邏輯也在工程和
計算機科學 中研究。
運算理論 基本理論 在布爾代數上的運算被稱為AND(與)、OR(或)和NOT(非)。
代數結構 要是布爾代數,這些運算的行為就必須和兩元素的布爾代數一樣(這兩個元素是TRUE(真)和FALSE(假))。亦稱邏輯代數.布爾(Boole,G.)為研究思維規律(邏輯學)於1847年提出的
數學工具 .布爾代數是指
代數系統 B=〈B,+,·,′〉
它包含集合B連同在其上定義的兩個
二元運算 +,·和一個
一元運算 ′,布爾代數具有下列性質:對B中任意元素a,b,c,有:
1.a+b=b+a, a·b=b·a.
2.a·(b+c)=a·b+a·c,
a+(b·c)=(a+b)·(a+c).
3.a+0=a, a·1=a.
4.a+a′=1, a·a′=0.
布爾代數也可簡記為B=〈B,+,·,′〉.在不致混淆的情況下,也將集合B稱作布爾代數.布爾代數B的集合B稱為布爾集,亦稱布爾代數的論域或
定義域 ,它是代數B所研究對象的全體.一般要求布爾集至少有兩個不同的元素0和1,而且其元素對三種運算+,·,′ 都封閉,因此並非任何集合都能成為布爾集.在有限集合的情形,布爾集的元素個數只能是2n,n=0,1,2,…二元運算+稱為布爾加法,布爾和,布爾並,布爾析取等;二元運算·稱為布爾乘法,布爾積,布爾交,布爾合取等;一元運算 ′ 稱為布爾補,布爾否定,布爾代數的余運算等.布爾代數的運算符號也有別種記法,如∪,∩,-;∨,∧,?等.由於只含一個元的布爾代數實用價值不大,通常假定0≠1,稱0為布爾代數的零元素或最小元,稱1為布爾代數的單位元素或最大元.布爾代數通常用
亨廷頓 公理系統來定義,但也有用
比恩 公理系統或具有0與1的有補分配格等來定義的。
例子 最簡單的布爾代數只有兩個元素 0 和 1,並通過如下規則(真值表)定義:
它套用於邏輯中,解釋 0 為假,1 為真,∧ 為與,∨ 為或,¬為非。涉及變數和
布爾運算 的表達式代表了陳述形式,兩個這樣的表達式可以使用上面的
公理 證實為等價的,
若且唯若 對應的陳述形式是邏輯等價的。
兩元素的布爾代數也是在電子工程中用於電路設計;這裡的 0 和 1 代表數字電路中一個位的兩種不同狀態,典型的是高和低電壓。電路通過包含變數的表達式來描述,兩個這種表達式對這些變數的所有的值是等價的,若且唯若對應的電路有相同的輸入-輸出行為。此外,所有可能的輸入-輸出行為都可以使用合適的
布爾表達式 來建模。
兩元素布爾代數在布爾代數的一般理論中也是重要的,因為涉及多個變數的等式是在所有布爾代數中普遍真實的,若且唯若它在兩個元素的布爾代數中是真實的(這總是可以通過平凡的蠻力
算法 證實)。比如證實下列定律(合意(Consensus)
定理 )在所有布爾代數中是普遍有效的:
(a ∨ b) ∧ (¬a ∨ c) ∧ (b ∨ c) ≡ (a ∨ b) ∧ (¬a ∨ c)
(a ∧ b) ∨ (¬a ∧ c) ∨ (b ∧ c) ≡ (a ∧ b) ∨ (¬a ∧ c)
任何給定集合 S 的冪集(
子集 的集合)形成有兩個運算 ∨ := ∪ (並)和 ∧ := ∩ (交)的布爾代數。最小的元素 0 是空集而最大元素 1 是集合 S 自身。
有限的或者 cofinite 的集合 S 的所有子集的集合是布爾代數。
對於任何
自然數 n,n 的所有
正約數 的集合形成一個分配格,如果我們對 a | b 寫 a ≤ b。這個格是布爾代數
若且唯若 n 是無平方因子的。這個布爾代數的最小的元素 0 是自然數 1;這個布爾代數的最大元素 1 是自然數 n。
布爾代數的另一個例子來自拓撲空間: 如果 X 是一個拓撲空間,它既是開放的又是閉合的,X 的所有子集的蒐集形成有兩個運算 ∨ := ∪ (並)和 ∧ := ∩ (交)的布爾代數。
如果 R 是一個任意的環,並且我們定義中心冪等元(central idempotent)的集合為
A = { e ∈ R : e2 = e,ex = xe,x ∈ R }
則集合 A 成為有兩個運算 e ∨ f := e + f + ef 和 e ∧ f := ef 的布爾代數。
布爾代數 二進制布爾代數 特性和示例 要使用布爾代數,必須了解布爾代數的特性:
元素是一個集合的成員。例如:A1,用A1 ∈ B表示。如果A1不是這個集合的元素,用A1 B表示。
子集是包含部分元素的集合,例如A,包含集合X中的元素A1,A2,用A∈B表示。
一元運算是對單個集合(例如A)進行運算,目的是求全集內除集合A以外的元素,用¬A表示。
二元運算是對兩個集合(例如A1、A2)進行運算,目的是:求兩個集合的共有元素,用A1∧A2表示;求兩個集合的所有元素,用A1∨A2表示。
了解了布爾代數的抽象化特性後,我們通過實例來介紹如何使用布爾代數進行集合運算。設定集合B中包含元素{1,2,3,4,5,6,7,8,9,10},子集A1中包含元素{1,2,3,4,5},子集A2中包含元素{3,4,5,7,10}。那么對應的運算結果為:
序理論 Image:Hasse diagram of powerset of 3.png
子集的布爾格同任何格一樣,布爾代數 (A,<math>\land</math>,<math>\lor</math>) 可以引出
偏序集 (A,≤),通過定義
a ≤ b
若且唯若 a = a <math>\land</math> b (它也等價於 b = a <math>\lor</math> b)。
事實上你還可以把布爾代數定義為有最小元素 0 和最大元素 1 的分配格 (A,≤) (考慮為
偏序集合 ),在其中所有的元素 x 都有補 ¬x 滿足
x <math>\land</math> ¬x = 0 並且 x <math>\lor</math> ¬x = 1
這裡的 <math>\land</math> 和 <math>\lor</math> 用來指示兩個元素的
下確界 (交)和
上確界 (並)。還有,如果上述意義上的補存在,則它們是可唯一確定的。
代數的和
序理論 的觀點通常可以交替的使用,並且二者都是有重要用處的,可從泛代數和序理論引入結果和概念。在很多實際例子中次序關係、
合取 (邏輯與)、
析取 (邏輯或)和否定(邏輯非)都是自然的可獲得的,所以可直接利用這種聯繫。
對偶原理 你還可以把來自
序理論 的對偶性的普遍認識套用於布爾代數。特別是,所有的布爾代數的次序對偶,或者等價的說通過對換 <math>\land</math> 與 <math>\lor</math> 所獲得的代數,也是布爾代數。一般的說,布爾代數的任何有效的規律都可以變換成另一個有效的對偶規律,通過對換 0 與 1,<math>\land</math> 與 <math>\lor</math>,和 ≤ 與 ≥。
其他記號 布爾代數的運算符可以用各種方式表示。它們經常簡單寫成 AND、OR 和 NOT。在描述電路時,還可以使用 NAND (NOT AND)、NOR (NOT OR) 和 XOR (排斥的 OR)。數學家、工程師和程式設計師經常使用 + 表示 OR 和 · 表示 AND (因為在某些方面這些運算類似於在其他
代數結構 中的加法和乘法,並且這種運算易於對普通代數熟悉的人得到積之和
範式 ),和把 NOT 表示為在要否定的表達式頂上畫一條橫線。
這裡我們使用另一種常見記號,"交" <math>\land</math> 表示 AND,"並" <math>\lor</math> 表示 OR,和 ¬ 表示 NOT。(使用只有文本的
瀏覽器 的讀者將見到 LaTeX 代碼而不是他們表示的楔形符號。)
同態和同構 在布爾代數 A 和 B 之間的同態是一個函式 f : A → B,對於在 A 中所有的 a,b 都有:
f(a <math>\lor</math> b) = f(a) <math>\lor</math> f(b)
f(a <math>\land</math> b) = f(a) <math>\land</math> f(b)
f(0) = 0
f(1) = 1
接著對於在 A 中所有的 a,f(¬a) = ¬f(a) 同樣成立。所有布爾代數的類,和與之在一起的
態射 (morphism)的概念,形成了一個範疇。從 A 到 B 的同構是
雙射 的從 A 到 B 的
同態 。
同態 的逆也是同態,我們稱兩個布爾代數 A 和 B 為同態的。從布爾代數理論的立場上,它們是不能區分的;它們只在它們的元素的符號上有所不同。
衍生理論 布爾環 每個布爾代數 (A,<math>\land</math>,<math>\lor</math>) 都引出一個環 (A,+,*),通過定義 a + b = (a <math>\land</math> ¬b) <math>\lor</math> (b <math>\land</math> ¬a) (這個運算在集合論中叫做"
對稱差 "在邏輯中叫做XOR(
異或 )) 和 a * b = a <math>\land</math> b。這個環的零元素符合布爾代數的 0;環的乘法單位元素是布爾代數的 1。這個環有對於 A 中的所有的 a 保持 a * a = a 的性質;有這種性質的環叫做
布爾環 。
反過來,如果給出
布爾環 A,我們可以把它轉換成布爾代數,通過定義 x <math>\lor</math> y = x + y + xy 和 x <math>\land</math> y = xy。因為這兩個運算是互逆的,我們可以說每個
布爾環 引發一個布爾代數,或反之。此外,映射 f : A → B 是布爾代數的
同態 ,
若且唯若 它是
布爾環 的同態。
布爾環 和代數的範疇是等價的。
布爾代數 A 的理想是一個子集 I,對於在 I 中的所有 x,y 我們有 x <math>\lor</math> y 在 I 中,並且對於在 A 中的所有 a 我們有 a <math>\land</math> x 在 I 中。理想的概念符合在布爾環 A
中環 理想的概念。A 的理想 I 叫做
素理想 ,如果 I ≠ A;並且如果 a <math>\land</math> b 在 I 中總是蘊涵 a 在 I 中或 b 在 I 中。A 的理想 I 叫做極大理想,如果 I ≠ A 並且真正包含 I 的唯一的理想是 A 自身。這些概念符合
布爾環 A 中的
素理想 和極大理想的環理論概念。
理想的對偶是
濾子 。布爾代數 A 的濾子是子集 p,對於在 p 中的所有 x,y 我們有 x <math>\land</math> y 在 p 中,並且對於在 A 中的所有 a,如果 a <math>\lor</math> x = a 則 a 在 p 中。
如何表示 可以證實所有的有限的布爾代數都同構於這個有限集合的所有子集的布爾代數。此外,所有的有限的布爾代數的元素數目都是二的冪。
Stone 的著名的布爾代數的表示
定理 陳述了所有的布爾代數 A 都在某個(緊湊的完全不連通的 Hausdorff)拓撲空間中同構於所有閉開集的布爾代數。
公理化 在 1933 年,
美國 數學家 Edward Vermilye Huntington (1874-1952) 展示了對布爾代數的如下公理化:
結合律 : (x + y) + z = x + (y + z)。
Huntington
等式 : n(n(x) + y) + n(n(x) + n(y)) = x。
Herbert Robbins 接著擺出下列問題: Huntington
等式 能否縮短為下述的等式,並且這個新等式與
結合律 和
交換律 一起成為布爾代數的基礎? 通過一組叫做 Robbins 代數的公理,問題就變成了: 是否所有的 Robbins 代數都是布爾代數?
結合律 : (x + y) + z = x + (y + z)。
Robbins
等式 : n(n(x + y') + n(x + n(y))) = x。
這個問題自從 1930 年代一直是公開的,並成為 Alfred Tarski 和他的學生最喜好的問題。
在 1996 年,William McCune 在 Argonne 國家實驗室,建造在 Larry Wos、Steve Winker 和 Bob Veroff 的工作之上,肯定的回答了這個長期存在的問題: 所有的 Robbins 代數都是布爾代數。這項工作是使用 McCune 的自動推理程式 EQP 完成的。
規則 代入法則 它可描述為邏輯
代數式 中的任何變數A,都可用另一個函式Z代替,等式仍然成立。
對偶法則 它可描述為對任何一個邏輯表達式F,如果將其中的“+”換成“*”,“*”換成“+”,“1”換成“0”,“0”換成“1”,仍保持原來的邏輯優先權,則可得到原函式F的對偶式G,而且F與G互為對偶式。我們可以看出基本公式是成對出現的,二都互為
對偶式 。
我們可以把反演法則這樣描述:將原函式F中的“*”換成“+”,“+”換成“*”,“0”換成“1”,“1”換成“0”;原變數換成反變數,反變數換成原變數,長非號即兩個或兩個以上變數的非號不變,就得到
原函式 的
反函式 。
定律 互補律:
第一互補律:若A=0,則~A=1,若A=1,則~A=0 註:~A =NOT A
第二互補律:A*~A=0
第三互補律:A+~A=1
雙重互補律:/<~A>=//A=A
交換律:
AND交換律:A*B=B*A
結合律:
AND結合律:A<B*C>=C*<A*B>
OR結合律: A+<B+C>=C+<A+B>
分配律:
第一分配律: A*<B+C>=<A*B>+<A*C>
第二分配律: A+<B*C>=<A+B>*<A+C>
重言律:
第一重言律: A*A=A 若A=1,則A*A=1;若A=0,則A*A=0。因此表達式簡化為A
第二重言律: A+A=A 若A=1,則1+1=1;若A=0,則0+0=0。因此表達式簡化為A
帶常數的重言律:
A+1=1
A*1=A
A*0=0
A+0=A
第一吸收率: A*<A+B>=A
第二吸收率: A+<A*B>=A
原型 在
k 元素集合
X 上有
k 個
n 元運算
f :
X →
X ,因此在{0,1}上有2個
n 元運算。所以得出所有布爾代數,不論大小都兩個常量或“零元”運算,四個一元運算,16個二元運算,256個三元運算,以此類推,它們叫做給定布爾代數的
布爾運算 。只有一個例外就是一個元素的布爾代數,它叫做退化的或平凡的(被一些早期作者禁用),布爾代數的所有運算可以被證明是獨特的。(在退化情況下,給定元數的所有運算都是同樣的運算因為對所有輸入都返回同樣結果。)
在{0,1}上的運算可以用
真值表 展出,選取0和1為真值
假 和
真 。它們可以按統一和不依賴套用的方式列出,允許我們命名或至少單獨列出它們。這些名字對布爾運算提供方便的簡寫。
n 元運算的名字是2位的二進制數。有2個這種運算,你不能得到更簡明的命名法了!
子集的布爾格的哈斯圖 下面展示元數從0到2的所有運算的這種格局和關聯的名字。
直到2元的布爾運算的真值表
常量
一元運算
二元運算
x 0x 1f 0f 1f 2f 3f 4f 5f 6f 7f 8f 9f 10f 11f 12f 13f 14f 150
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
這些表格繼續到更高元數上,對n 元有2行,每個行給出n 個變數x 0,…x n −1的一個求值或綁定,而每列都有表頭f i ,它們給出第i 個n 元運算f i (x 0,…,x n −1)在這個求值下的值。運算包括變數本身,例如f 2是x 0而f 10是x 0 (作為它的一元對應者的兩個復件)而f 12是x 1 (沒有一元對應者)。否定或補¬x 0齣現為f 1再次出現為f 5,連同f 3 (¬x 1在1元時沒有出現),析取或並x 0∨x 1出現為f 14,合取或交x 0∧x 1出現為f 8,蘊涵x 0→x 1出現為f 13,異或或對稱差x 0⊕x 1出現為f 6,差集x 0−x 1出現為f 2等等。對布爾函式的其他命名或表示可參見零階邏輯。
作為關於它的形式而非內容的次要詳情,一個代數的運算傳統上組織為一個列表。我們這裡通過在{0,1}上有限運算索引了布爾代數的運算,上述真值表表示的排序首先按元數,其次為每個元數運算的列出表格。給定元數的列表次序是如下兩個規則確定的。
套用領域 套用
布爾代數不僅可以在數學領域內實現集合運算,更廣泛套用於
電子學 、
計算機 硬體、計算機軟體等領域的邏輯運算:當集合內只包含兩個元素(1和0)時,分別對應{真}和{假},可以用於實現對邏輯的判斷。
常見的套用包括:
數字電路 設計,0和1與數字電路中某個位的狀態對應,例如:高
電平 、低電平。
計算機的
網路 設定,利用計算機的
二進制 特性,將
子網掩碼 與本機
IP 地址進行邏輯與運算,可以得到計算機的網路地址和主機地址。
資料庫 套用,通過
SQL 語句查詢資料庫時需要進行邏輯運算,確定具體的查詢目標。
 布爾代數
布爾代數 數學家G.布爾
數學家G.布爾 德·摩根
德·摩根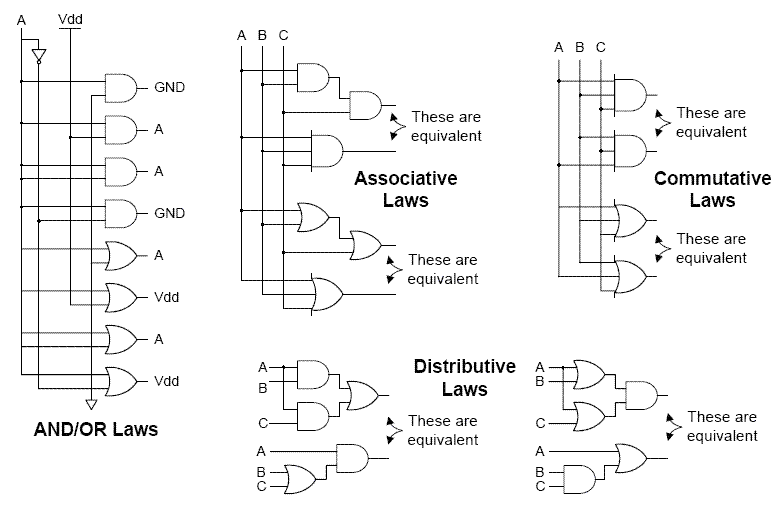 布爾代數
布爾代數 二進制布爾代數
二進制布爾代數
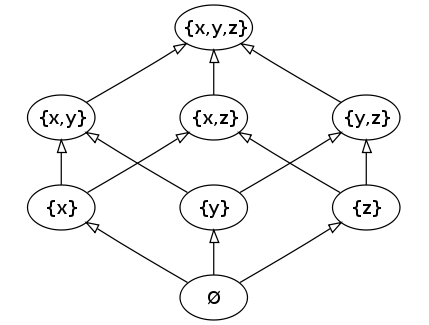 子集的布爾格的哈斯圖
子集的布爾格的哈斯圖
 離散數學
離散數學