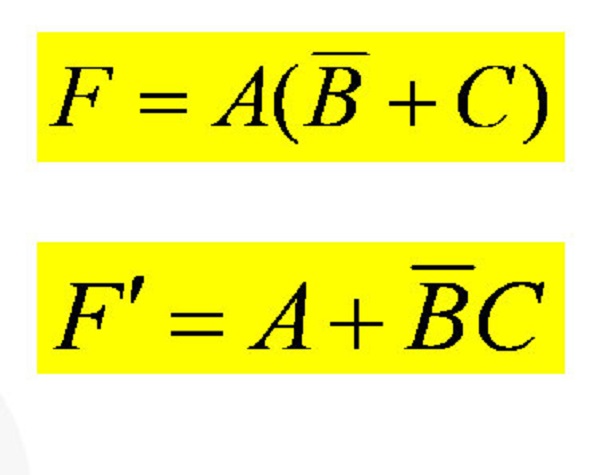對偶式

在邏輯代數中的對偶式：如果將邏輯函式表達式F中所有的“·”變成“+”，“+”變成“·”，“0”變成“1”，“1”變成“0”，並保持原函式中的運算順序不變，則所得到的新的邏輯表達式稱為函式F的對偶式，並記作F'。

基本介紹

• 中文名：對偶式
• 外文名：Duality
• 簡介：所得到的新的邏輯表達式
• 特例：函式F為自對偶函式
• 注意：等式兩端表達式的對偶式也相等

對偶式簡介

在邏輯代數中的對偶式：如果將邏輯函式表達式F中所有的“·”變成“+”，“+”變成“·”，“0”變成“1”，“1”變成“0”，並保持原函式中的運算順序不變，則所得到的新的邏輯表達式稱為函式F的對偶式，並記作F'。 例如，F=AB+B(C+0) F'=(A+B)(B+C·1) ，從例子可以看出，如果F的對偶式是F'，則F'的對偶式就是F。即，F和 F'互為對偶式。

若邏輯函式表達式的對偶式就是原函式表達式本身，即F'=F。則稱函式F為自對偶函式。 例如，函式 是一自對偶函式。因為：F'=(A·C+B)·(A+B·C) =(A+B)(C+B)(A+B)(A+C) =A(B+C)(A+C)+B(B+C)(A+C) =(B+C)(A+AC)+(B+B·C)(A+C) =A(B+C)+B(A+C) =F 求某一邏輯表達式的對偶式時，同樣要注意保持原函式的運算順序不變。

若兩個邏輯函式表達式F和G相等，則其對偶式F'和G'也相等。這一規則稱為對偶規則。根據對偶規則，當已證明某兩個邏輯表達式相等時，便可知道它們的對偶式也相等。例如，已知AB+AC+BC=AB+AC。
根據對偶規則可知等式兩端表達式的對偶式也相等，即有：(A+B)·(A+C)·(B+C)=(A+B)(A+C)

對偶式定理

在命題邏輯中的對偶式：在僅含有聯結詞與（∧）、或（∨）、非（┐）的命題公式A中，將∨換成∧，∧換成∨，若A中還含有0或1，則還需將其中的0換成1，1換成0，，所得到的新命題公式A*就是A的對偶式。例如，命題公式A=┐(P∧0)的對偶式A*=┐(P∨1)。

定理1：A和A*是互為對偶式，P，P2，...，Pn是出現在A和A*的原子變元，則 ┐A(P,...,Pn) <=> A*┐P,...┐Pn)； A(┐P,...Pn) <=> ┐A*(P,...,Pn)；即公式的否定等值於其變元否定的對偶式。例子：De Morgan定律 ┐(P∧Q)=┐P∨┐Q。

定理2：設A*，B*分別是A和B的對偶式，如果A<=>B，則A*<=>B*。這就是對偶原理。如果證明了一個等值公式，其對偶式的等值同時也立。可以起到事半功倍的效果。