基本介紹
- 中文名:對偶定理
- 外文名:Duality theorem
- 所屬領域:數理科學
定義
舉例
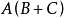
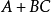
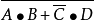
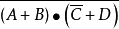
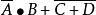
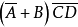
性質定理與推論
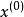
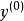

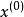
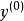
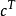
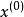
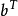
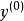
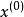
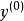
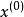
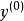
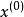
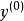
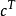
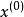
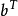
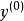



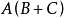
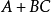
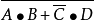
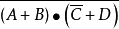
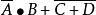
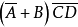
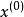
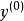

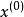
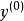
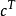
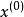
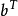
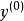
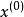
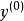
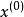
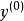
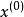
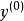
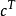
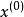
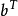
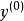


對偶定理是一個數學術語,指的是若兩邏輯式相等,則它們的對偶式也相等。對偶式指的是對於任何一個邏輯式Y,若將其中的“·”換成“+”,“+”換成“·”,0換...
對偶原理,又叫對偶原則。對偶原理是指在射影空間中,若一個命題成立,則其對偶命題也必成立。...
對偶理論是研究線性規劃中原始問題與對偶問題之間關係的理論。 線上性規劃早期發展中最重要的發現是對偶問題,即每一個線性規劃問題(稱為原始問題)有一個與它對應的...
在數學中,以亨利·龐加萊(Henri Poincaré)命名的龐加萊對偶性定理是流形結構的基本結果。 它指出,如果M是一個n維定向的閉合流形(緊湊而沒有邊界),則M的第k...
若原始問題(對偶問題)有一個確定的最優解,那么對偶問題(原始問題)也有一個確定的最優解,而且這兩個最優解所對應的目標函式值相等,這就是強對偶性。...
塞爾對偶定理(Serre duality theorem)是複流形上全純向量叢與對偶向量叢的上同調群同構的定理。...
對偶是大自然中廣泛存在的,呈“分形”形態分布的一種結構規律,及任何系統往下和往上均可找出對偶二象的結構關係,且二象間具有完全性、互補性、對立統一性、穩定...
在邏輯代數中的對偶式:如果將邏輯函式表達式F中所有的“·”變成“+”,“+”變成“·”,“0”變成“1”,“1”變成“0”,並保持原函式中的運算順序不變,則...
龐特里亞金對偶性定理(Pontryagin dualitytheorem)是關於局部緊交換群與其對偶群的同構定理。...
對偶擬陣(dual matroid)亦稱正交擬陣,是一種組合構形,它是由擬陣M導出的擬陣M*,當擬陣M以基集族B表示時,M=(E,B),則M*=(E,B*),其中B*={E-B:B∈B...
森田紀一對偶定理(Morita theorem on duali-ty)模範疇對偶性的重要定理...... 森田紀一對偶定理(Morita theorem on duali-ty)模範疇對偶性的重要定理.森田紀一...
惠特尼對偶定理(Whitney duality theorem)是微分流形的切叢與餘切叢的施蒂費爾-惠特尼類的關係。...
每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。...
代數對偶(algebraic duality)是射影幾何的一個術語,即採用齊次坐標後,用雙線性齊次方程表示圖形的對偶性,例如在二維射影空間,方程u1x1+u2x2+u3x3=0表示直線[u1...
將∪ 和∩,或者 Ø 和 U 相互交換,一個恆等式就變成了相應的另一個。 這是集合代數的一個非常重要的性質,稱作集合的對偶性原理。它對集合的所有真命題...
戴維南定理(Thevenin's theorem):含獨立電源的線性電阻單口網路N,就連線埠特性而言,可以等效為一個電壓源和電阻串聯的單口網路。電壓源的電壓等於單口網路在負載開路時...
在泛函分析中,哈恩-巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間,並說明了存在「足夠」的連續線性泛函,定義在每...
對偶規劃(dual programming)一類線性規劃問題,指由原線性規劃問題按如下對稱規律構成的新線性規劃問題:若原問題(P)為maxz=CTX,滿足{AX≤b,x≤0 },則對稱的新...
布列安桑(Brianchon)定理是一個射影幾何中的著名定理,它斷言六條邊和一條圓錐曲線相切的六邊形的三條對角線共點,此點被稱為該六邊形的布列安桑點。...
對偶網路是網路的一種類型。如果有兩個網路N和Nz,它們的支路一一對應,其中一個網路的支路電壓或電流的每一種約束關係,是另一個網路中相應支路把電壓與電流互換...
對偶元素是射影幾何的一個術語,指射影幾何中元素間的一種特殊關係。在歐氏幾何中,幾何圖形是點的軌跡,是把點作為圖形基本元素,而射影幾何認為圖形可看成是直線...
對偶原則,又稱為對偶原理。是射影幾何的一個基本原則,指在射影空間中,若一個命題成立,則其對偶命題也必成立。...
巴比涅原理 :在夫琅禾費衍射中,兩個振幅型互補的衍射屏在接收屏上的遠離衍射...巴俾涅原理指出,滿足互補條件的問題是一對偶問題,其場分布滿足對偶原理。...
