每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。對偶問題的最優解也可以通過原問題的最優解得到,反之亦然。而且,在某些情況下,利用對偶理論求解線性規劃問題更為簡單,而且有助於深入了解待求問題的本質。
基本介紹
- 中文名:對偶線性規劃
- 外文名:dual linear programming
- 套用學科:數學術語
- 範疇:數理科學
- 解法:對偶單純形法
- 涉及:對偶問題
概述
基本性質
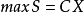
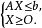

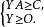

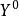

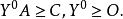

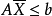
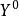
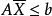
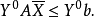


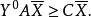


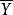

每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。對偶問題的最優解也可以通過原問題的最優解得到,反之亦然。而且,在某些情況下,利用對偶理論求解線性規劃問題更為簡單,而且有助於深入了解待求問題的本質。
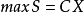
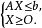

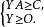

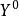

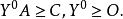

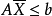
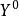
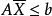
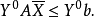


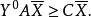


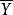
每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。...
對偶理論是研究線性規劃中原始問題與對偶問題之間關係的理論。 在線性規劃早期發展中最重要的發現是對偶問題,即每一個線性規劃問題(稱為原始問題)有一個與它對應的...
對偶規劃(dual programming)一類線性規劃問題,指由原線性規劃問題按如下對稱規律構成的新線性規劃問題:若原問題(P)為maxz=CTX,滿足{AX≤b,x≤0 },則對稱的新...
線性規劃的對偶理論指研究線性規劃問題和它對應的對偶問題之間存在的變數、係數及數學符號的嚴格對應關係的理論。線性規劃的對偶理論,不僅存在於原始問題與對偶問題的...
線性規劃(Linear programming,簡稱LP)是運籌學中研究較早、發展較快、套用廣泛、方法較成熟的一個重要分支,它是輔助人們進行科學管理的一種數學方法。研究線性約束...
混合型對偶線性規劃(mixed type dual linearprogramming)一類對偶線性規劃(問題).稱 是互為混合型對偶線性規劃(問題). ...
《線性規劃第二版》是2007年武漢大學出版社出版的圖書,作者是張乾宗。本書是在借鑑已有教材並結合筆者教學實踐積累的基礎上編寫的。...
線性規劃中的套用每一個規劃問題都存在一個與它相關的對偶問題。原問題中的約束條件的個數等於對偶問題的變數的個數;原問題中變數的個數等於對偶問題中約束條件的...
線性規劃問題又稱線性規劃,在數學中線性規劃(Linear Programming,簡稱LP)特指目標函式和約束條件皆為線性的最最佳化問題。...
對偶理論是從數量關係上研究這些對偶問題的性質、關係及其套用的理論和方法。每一個線性規劃問題,都存在一個與之相聯繫的對偶問題。 [1] ...
對偶變數(dual variable)對偶線性規劃問題中的變數(參見“對稱形式的對偶線性規劃”). ...
全對偶整數性(total dual integrality)組合最佳化問題的一種性質。指線性規劃max Z=c,滿足Ax=b具有如下性質:矩陣A及向量b均取整數值,而且對於任意的整數向量。此...
凸規劃對偶問題(dual problem of convex pro-gramming)一類綜合的對偶問題.指線性規劃、帶凸性的非線性規劃和二次規劃的對偶問題的綜合形式...
對偶理論是研究線性規劃中原始問題與對偶問題之間關係的理論。 在線性規劃早期發展中最重要的發現是對偶問題,即每一個線性規劃問題(稱為原問題)有一個與它對應的...
本書內容包括:線性規劃問題的數學模型、線性規劃問題的數學模型、線性規劃問題解的性質、兩個變數的線性規劃問題的圖解法、線性規劃問題的標準形式、線性規劃問題解的...
當求目標函式的最小值時,改進的數量應該是減少的數量,所以影子價格即為負的對偶價格。影子價格又稱影子利率用線性規劃方法求解資源最優利用時,即在解決如何使有限...
原始-對偶方法是求解線性規劃的一種算法,指求解線性規劃的一類特殊對偶型方法,其特殊性在於,它是以鬆弛互補性條件為基礎去構造一個由原問題產生的限定問題,並通過...
《線性規劃及其理論基礎》是2009年中央廣播電視大學出版社出版的圖書,圖書作者是董秀媛。...
參數線性規劃(parametric linear programm-ing)數學規劃的一個分支.它研究係數不是常數,而是在某範圍內變化的參數的線性規劃問題.求解參數線性規劃問題的目的就是求出...
