對偶性是描述導致相同的物理結果,表面上不同的理論之間的對應關係。這種對應關係在信號與系統理論中主要體現在函式x(t)的傅立葉變換X(jw)和函式X(t)的傅立葉變換x(jw)的關係中。
基本介紹
- 中文名:對偶性
- 外文名:Duality
- 出處:《時間簡史》
- 結果:導致相同的物理結果
- 表現:表面上不同的理論之間的對應
- 套用:物理和數學
定義
套用
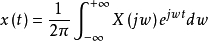
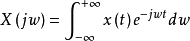
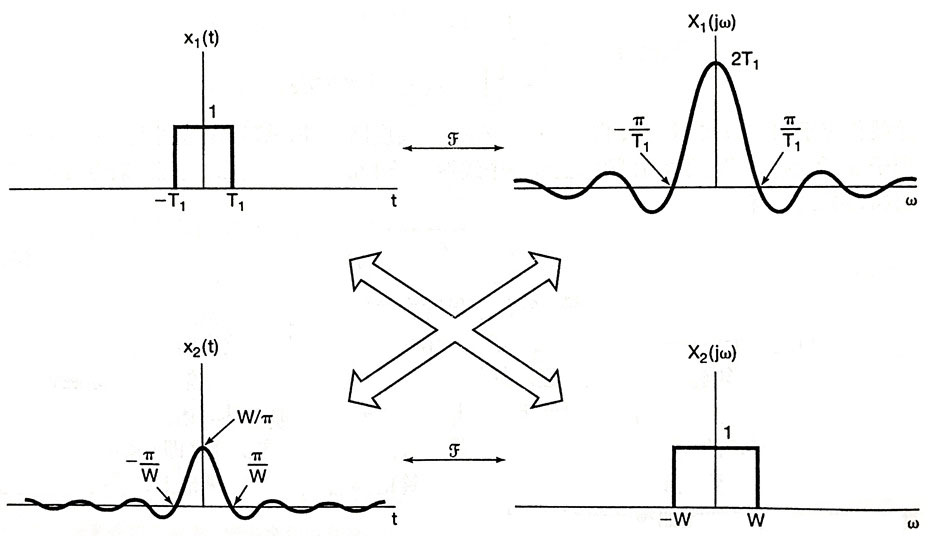
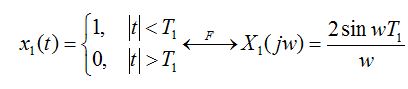 傅立葉變換1
傅立葉變換1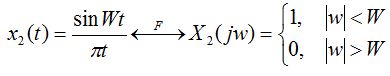 傅立葉變換2
傅立葉變換2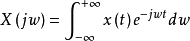
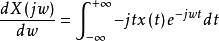
 公式
公式
對偶性是描述導致相同的物理結果,表面上不同的理論之間的對應關係。這種對應關係在信號與系統理論中主要體現在函式x(t)的傅立葉變換X(jw)和函式X(t)的傅立葉變換x(jw)的關係中。
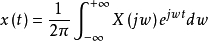
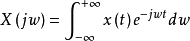
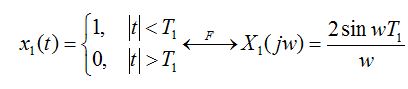 傅立葉變換1
傅立葉變換1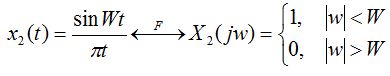 傅立葉變換2
傅立葉變換2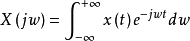
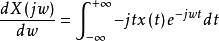
 公式
公式
對偶性是描述導致相同的物理結果,表面上不同的理論之間的對應關係。這種對應關係在信號與系統理論中主要體現在函式x(t)的傅立葉變換X(jw)和函式X(t)的傅立葉...
每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。...
在數學中,以亨利·龐加萊(Henri Poincaré)命名的龐加萊對偶性定理是流形結構的基本結果。 它指出,如果M是一個n維定向的閉合流形(緊湊而沒有邊界),則M的第k...
對偶性質(duality property)是廣義等周問題解的一種性質。類似於周長一定時面積最大的矩形和面積一定時周長最小的矩形的解都是正方形。...
龐特里亞金對偶性定理(Pontryagin dualitytheorem)是關於局部緊交換群與其對偶群的同構定理。...
將∪ 和∩,或者 Ø 和 U 相互交換,一個恆等式就變成了相應的另一個。 這是集合代數的一個非常重要的性質,稱作集合的對偶性原理。它對集合的所有真命題...
混合型對偶線性規劃(mixed type dual linearprogramming)一類對偶線性規劃(問題).稱 是互為混合型對偶線性規劃(問題). ...
偶性,是霍布斯提出來的另一個重要的哲學範疇,偶性不是事物可有可無的性質,而是指事物的一切性質。...
對偶理論是研究線性規劃中原始問題與對偶問題之間關係的理論。 線上性規劃早期發展中最重要的發現是對偶問題,即每一個線性規劃問題(稱為原始問題)有一個與它對應的...
對偶定理是一個數學術語,指的是若兩邏輯式相等,則它們的對偶式也相等。對偶式指的是對於任何一個邏輯式Y,若將其中的“·”換成“+”,“+”換成“·”,0換...
最優性,運籌學中的術語,對偶問題的基本性質之一。如果X是原問題的可行解,Y是對偶問題的可行解,並且CX=Yb,那么X和Y分別為原問題和對偶問題的最優解。這個定理...
可鎮定性Popov-Belevitch-Hautus判據根據對偶性,可得到可檢性的判據為:下列命題是等價的:1.矩陣對(A,C)是可檢的。2.不存在A的非負實部特徵值對應的右特徵...
Hough變換是利用圖像全局特性而將邊緣像素連線起來組成區域封閉邊界的一種方法,其基本思想是點—線的對偶性;邊界方向直方圖法首先微分圖像求得圖像邊緣,然後,做出關於...
主要內容包括變分分析的相關基礎、約束集合的切錐與二階切集、對偶理論、非線性錐約束最佳化的一階最優性條件和二階最優性條件、三類重要的錐約束最佳化的最優性條件...
15.對偶性的其他問題第6章 運輸問題16.第1階段17.第2階段18.工作指派問題第7章 矩陣對策19.什麼是矩陣對策20.矩陣對策與線性規劃...
第5童 線性系統的能控性和能觀測性5.1 能控性定義及其判據5.2 能觀測性定義及其判據5.3 對偶性原理5.4 線性離散時間系統能控性和能觀測性...
8.4.3 對偶性8.4.4 定常情況的特徵描述8.4.5 不可觀部分的刪除8.4.6 離散時間系統的可觀測性8.5 線性定常系統的最小實現8.5.1 最小性...
1.1 能控性定義1.2 能控性判據1.3 能控性指數1.4 能控性子空間§2 線性系統的能觀性2.1 能觀性定義2.2 對偶性原理2.3 不能觀子空間§3 線性系統...
