對偶性質(duality property)是廣義等周問題解的一種性質。類似於周長一定時面積最大的矩形和面積一定時周長最小的矩形的解都是正方形。
基本介紹
- 中文名:對偶性質
- 外文名:duality property
- 適用範圍:數理科學
簡介
具體內容
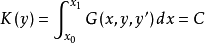
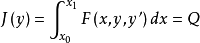
廣義等周問題
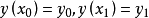
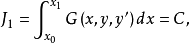

對偶性質(duality property)是廣義等周問題解的一種性質。類似於周長一定時面積最大的矩形和面積一定時周長最小的矩形的解都是正方形。
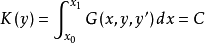
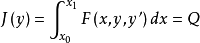
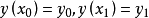
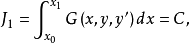

對偶性質(duality property)是廣義等周問題解的一種性質。類似於周長一定時面積最大的矩形和面積一定時周長最小的矩形的解都是正方形。...
對偶性是描述導致相同的物理結果,表面上不同的理論之間的對應關係。這種對應關係在信號與系統理論中主要體現在函式x(t)的傅立葉變換X(jw)和函式X(t)的傅立葉...
對偶定理是一個數學術語,指的是若兩邏輯式相等,則它們的對偶式也相等。對偶式指的是對於任何一個邏輯式Y,若將其中的“·”換成“+”,“+”換成“·”,0換...
對偶是大自然中廣泛存在的,呈“分形”形態分布的一種結構規律,及任何系統往下和往上均可找出對偶二象的結構關係,且二象間具有完全性、互補性、對立統一性、穩定...
對偶原則,又稱為對偶原理。是射影幾何的一個基本原則,指在射影空間中,若一個命題成立,則其對偶命題也必成立。...
對偶問題是實質相同但從不同角度提出不同提法的一對問題。對偶現象是許多管理與工程實際中存在的一種普遍現象。例如,企業怎樣充分利用現有人力、物力去完成更多的...
對偶理論是研究線性規劃中原始問題與對偶問題之間關係的理論。 線上性規劃早期發展中最重要的發現是對偶問題,即每一個線性規劃問題(稱為原始問題)有一個與它對應的...
對偶元素是射影幾何的一個術語,指射影幾何中元素間的一種特殊關係。在歐氏幾何中,幾何圖形是點的軌跡,是把點作為圖形基本元素,而射影幾何認為圖形可看成是直線...
對偶規劃(dual programming)一類線性規劃問題,指由原線性規劃問題按如下對稱規律構成的新線性規劃問題:若原問題(P)為maxz=CTX,滿足{AX≤b,x≤0 },則對稱的新...
代數對偶(algebraic duality)是射影幾何的一個術語,即採用齊次坐標後,用雙線性齊次方程表示圖形的對偶性,例如在二維射影空間,方程u1x1+u2x2+u3x3=0表示直線[u1...
對偶婚,亦稱對偶家庭。指原始社會時期,不同氏族的成年男女雙方,在或長或短的時間內實行由一男一女組成配偶,以女子為中心,婚姻關係不穩固的一種婚姻形式。對偶婚...
每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。...
將∪ 和∩,或者 Ø 和 U 相互交換,一個恆等式就變成了相應的另一個。 這是集合代數的一個非常重要的性質,稱作集合的對偶性原理。它對集合的所有真命題...
對偶網路是網路的一種類型。如果有兩個網路N和Nz,它們的支路一一對應,其中一個網路的支路電壓或電流的每一種約束關係,是另一個網路中相應支路把電壓與電流互換...
對偶不變性指對偶線性空間相容拓撲不變的性質。集合的有界性就是一個對偶不變的性質。...
對偶根((dual radical)由補根導出的一個概念.若男和S是兩個根性質,其中每一個是另一個的補根,則稱(U}r' , .S})是補根的一個對偶對,而稱這兩個根中...
對偶擬陣(dual matroid)亦稱正交擬陣,是一種組合構形,它是由擬陣M導出的擬陣M*,當擬陣M以基集族B表示時,M=(E,B),則M*=(E,B*),其中B*={E-B:B∈B...
在數學裡,任何向量空間V都有其對應的對偶向量空間(或簡稱為對偶空間),由V的線性泛函組成。此對偶空間俱有一般向量空間的結構,像是向量加法及標量乘法。由此定義的...
對偶函子(dual functor)是對偶範疇間的一個顯見函子。即刻畫範疇C與C°間關係的一個標準函子。函子是範疇間的一類特殊映射。有些問題中需研究兩個範疇間的...
龐特里亞金對偶性定理(Pontryagin dualitytheorem)是關於局部緊交換群與其對偶群的同構定理。...
對偶向量族(dual family of vectors)是分別來自賦范線性空間與其共軛空間的滿足一定條件的一對子集。...
對偶曲線(dual curve)是研究平面代數曲線的一個重要工具。設C是射影平面中次數m>1的不可約曲線。C的所有非奇異點的切線的全體確定了對偶平面上的一個集合,它的...
函式變換對偶式,屬於數學語言。...... 反映二元域GF(2)上序列之間平移跨距關係的對偶函式,研究了基於二元域GF(2)上多項式f(x)對偶函式的存在性和若干性質,證明了...
