代數對偶(algebraic duality)是射影幾何的一個術語,即採用齊次坐標後,用雙線性齊次方程表示圖形的對偶性,例如在二維射影空間,方程u1x1+u2x2+u3x3=0表示直線[u1,u2,u3]的方程,其上的動點為(x1,x2,x3),方程x1u1+x2u2+x3u3=0是點(x1,x2,x3)的方程,過該點的動直線為[u1,u2,u3],而點和直線是二維射影空間的對偶元素。同理,在三維射影空間,方程α1x1+α2x2+α3x3+α4x4=0表示平面[α1,α2,α3,α4]的方程,其上的動點為(x1,x2,x3,x4),方程x1α1+x2α2+x3α3+x4α4=0表示點(x1,x2,x3,x4)的方程,過這點的動平面為[α1,α2,α3,α4],而點和平面是三維射影空間的對偶元素。
基本介紹
- 中文名:代數對偶
- 外文名:algebraic duality
- 所屬學科:數學
- 所屬問題:高等幾何(射影幾何)
基本介紹
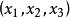
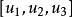
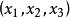
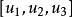
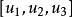
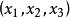
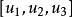
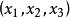
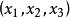
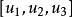
舉例說明
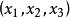

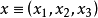
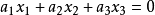
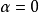
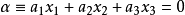
定理1 兩點a,b重合的充要條件是矩陣 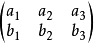 | 定理1' 兩直線α=0,β=0重合的充要條件是矩陣 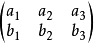 |
定理2兩個不同點a, b的連線的齊次方程是 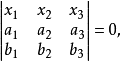 | 定理2'兩條不同直線α=0,β=0的交點的齊次坐標是 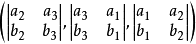 |
定理3 三個不同點共線的充要條件是其坐標所構成矩陣或其方程係數方陣的秩是2。即:三個不同點a, b, c共線的充要條件是 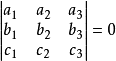 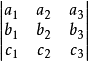 | 定理3' 三條不同直線共點的充要條件是其坐標所構成矩陣或其方程係數方陣的秩是2。即:三條不同直線α=0, β=0, γ=0共點的充要條件是 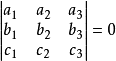 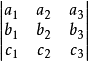 |
定理4 以兩個不同點a與b的連線為底的點列的點的坐標能且僅能寫作la+mb 。或以兩個不同點α=0與β=0的連線為底的點列的點的方程能且僅能寫作lα+ mβ= 0,這裡l,m為不全為零的常數。 | 定理4' 以兩條不同直線a與b的交點為中心的線束的直線的坐標能且僅能寫作la+ mb 。或以兩條不同直線α=0與β=0的交點為中心的線束的直線的方程能且僅能寫作Iα+mβ=0,這裡l,m為不全為零的常數。 |
推論 三個不同點a,b,c共線的充要條件是:有三個全不為零的常數p,q,r使pai+ qbi+rci= 0,或三個不同點α= 0,β=0,γ=0共線的充要條件是: 有三個全不為零的常數p,q, r而使pα+qβ+rγ= 0。 | 推論 三條不同直線a,b,c共點的充要條件是:有三個全不為零的常數p, q,r使pai+ qbi+rci= 0或三條不同直線α= 0,β=0,γ=0共點的充要條件是有三個全不為零的常數p,q, r使pα+qβ+rγ= 0。 |

