基本介紹
- 中文名:對偶空間
- 外文名:Dual Vector Space
- 套用學科:數學等
- 適用領域範圍:泛函分析
- 定義:行向量與列向量的關係的抽象化
- 相關術語:線性函式
簡介
定義
線性函式
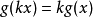
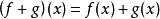
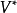
雙對偶空間
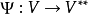
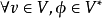
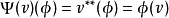
有限維的情形
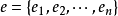

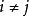
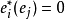
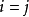
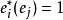
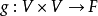
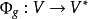
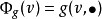
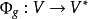
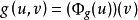
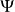
無限維的情形
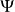
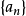
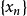
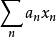
張量代數
線性映射轉置
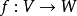
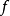
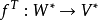
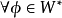
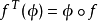

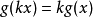
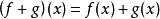
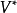
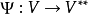
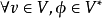
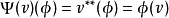
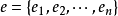

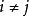
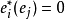
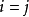
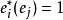
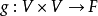
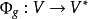
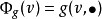
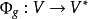
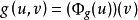
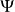
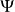
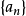
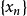
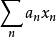
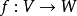
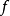
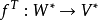
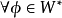
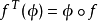
在數學裡,任何向量空間V都有其對應的對偶向量空間(或簡稱為對偶空間),由V的線性泛函組成。此對偶空間俱有一般向量空間的結構,像是向量加法及標量乘法。由此定義的...
對偶空間圖是線性空間的一個定義。...... (a),(kf)(a)=kf(a),則L(V,P)也是數域P上的線性空間.這樣構造的L(V,P)就稱為V的對偶空間. 對偶空間圖 - ...
在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名,儘管依據Bourbaki (1987)...
本書主要內容包括:預備知識、LP空間、Lorentz空間與Orlicz空間、Sobolev空間Ⅱ、有界變差函式等。...
對偶映射(dual mapping),數學專業術語,亦稱轉置映射。一種特殊的線性映射。是指線性代數中共扼變換的推廣。由對偶關係確定的從巴拿赫空間到其對偶空間的集值映射。...
《二象對偶空間與管理學二象論》是2005年科學出版社出版的圖書,作者是徐飛、高隆昌。...
一個把向量映射到非負實數的函式如果滿足簡介中描述的性質,就叫做一個半範數;如果只有零向量的函式值是零,那么叫做範數。擁有一個範數的向量空間叫做賦范向量空間,...
帳篷空間(tent space)是一類聯繫著面積積分與卡爾松測度的函式空間。...... 的對偶空間是卡爾松測度空間。 [1] 帳篷空間卡爾松測度 編輯 在數學中,卡爾松測度是對維...
伯格曼空間(Bergman space)是區域上平方可積的解析函式空間。數學中,函式空間指的是從集合 X 到集合 Y 的給定種類的函式的集合。其叫做空間的原因是在很多套用中...
布洛赫空間(Bloch space)一類重要的解析函式空間。解析函式是指能局部展成冪級數的函式,它是複變函數論研究的主要對象。解析函式類包括了數學及其在自然科學和技術...
擬桶型空間(quasi-barreled space)是桶型空間概念的推廣,設E是局部凸空間,E中的子集A稱為擬桶集,是指A是吸收一切有界集的桶集,如果E中每個擬桶集都是零元...
數學中,函式空間指的是從集合 X 到集合 Y 的給定種類的函式的集合。其叫做空間的原因是在很多套用中,它是拓撲空間或向量空間或這二者。經典分析學研究中出現了...
價格空間(price space)商品空間的對偶空間.它用來刻畫所研究的經濟問題中的價格.所謂價格或價格體系就是對每種商品指定一個價格.當商品空間為R”時,價格體系也可以...
k空間是尋常空間在傅利葉轉換下的對偶空間,主要套用在磁振造影的成像分析,其他如磁振造影中的射頻波形設計,以及量子計算中的初始態準備亦用到k空間的概念。k和...
定義 設V是實數集R上的有限維矢量空間,線性映射ω:V→R稱為R上的對偶矢量(dual vector)。V上全體對偶矢量的集合稱為V的對偶空間。 ...
對偶是大自然中廣泛存在的,呈“分形”形態分布的一種結構規律,及任何系統往下和往上均可找出對偶二象的結構關係,且二象間具有完全性、互補性、對立統一性、穩定...
有對偶空間 ,對偶群可看成 。更抽象的說,這兩者都是可表函子,被 及 所表示。定理:二次對偶 與 有個自然同構。在此,“自然”或“典範”同構意謂一個“自然...
對偶格是向量格到實數域R的序有界線性運算元全體。克列因等人證明了巴拿赫格的序性質如何確定了對偶格的序性質。...
對偶範數是泛函分析中的一個概念,代表一種測度或者距離,與範數的含義一致,表示一個數。考慮一個賦范向量空間的對偶空間時,常常需要給對偶空間賦以合適的幾何架構。...
在數學裡,尤其是在泛函分析之中,巴拿赫空間是一個完備賦范向量空間。更精確地說,巴拿赫空間是一個具有範數並對此範數完備的向量空間。...
BMO空間是有界平均振動空間的簡稱。...... 它包含著空間L∞(Rn),又是哈代空間H1(Rn)的對偶空間。詞條圖冊 更多圖冊 詞條標籤: 技術 V百科往期回顧 詞條統計 ...
對偶,在不同的領域有著不同的詮釋。在詞語中,它是一種修辭方法,兩個字數相等、結構相似的語句表現相反的意思。在語文中,對偶的種類很多,分為單句對偶、偶句對偶...
對偶錐((dual cone)亦稱極錐,錐的極集。有時對偶錐也稱為負極錐,相應地也可定義正極錐。實線性空間的理論常可推廣到凸錐的情形,即通常的向量的線性組合概念可...
全對偶整數性(total dual integrality)組合最佳化問題的一種性質。指線性規劃max Z=c,滿足Ax=b具有如下性質:矩陣A及向量b均取整數值,而且對於任意的整數向量。此...
速降函式空間(Schwartz space)是數學中一類函式的總稱,也稱為施瓦茨空間,指的是當自變數的值趨向於無窮大時,函式值趨近0的速度“足夠快”的函式。速降函式空間的...
對偶函子(dual functor)是對偶範疇間的一個顯見函子。即刻畫範疇C與C°間關係的一個標準函子。函子是範疇間的一類特殊映射。有些問題中需研究兩個範疇間的...
索伯列夫空間是數學裡由函式組成的賦范向量空間,主要用來研究偏微分方程理論,它以前蘇聯數學家С.Л.索伯列夫命名。...
