基本介紹
釋義
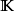
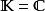
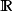
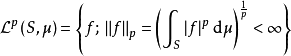

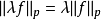



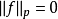
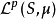

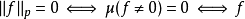
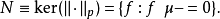
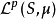
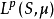
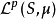
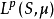
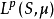

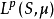


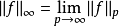
特例

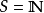

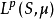
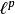
性質
對偶空間
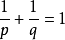
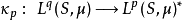
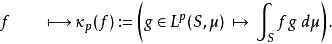
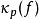
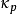
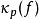
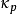
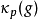
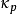
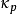
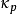

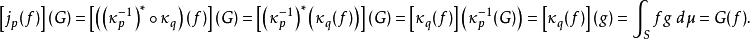
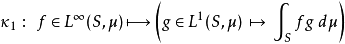
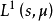
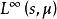
嵌入
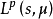
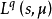

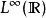
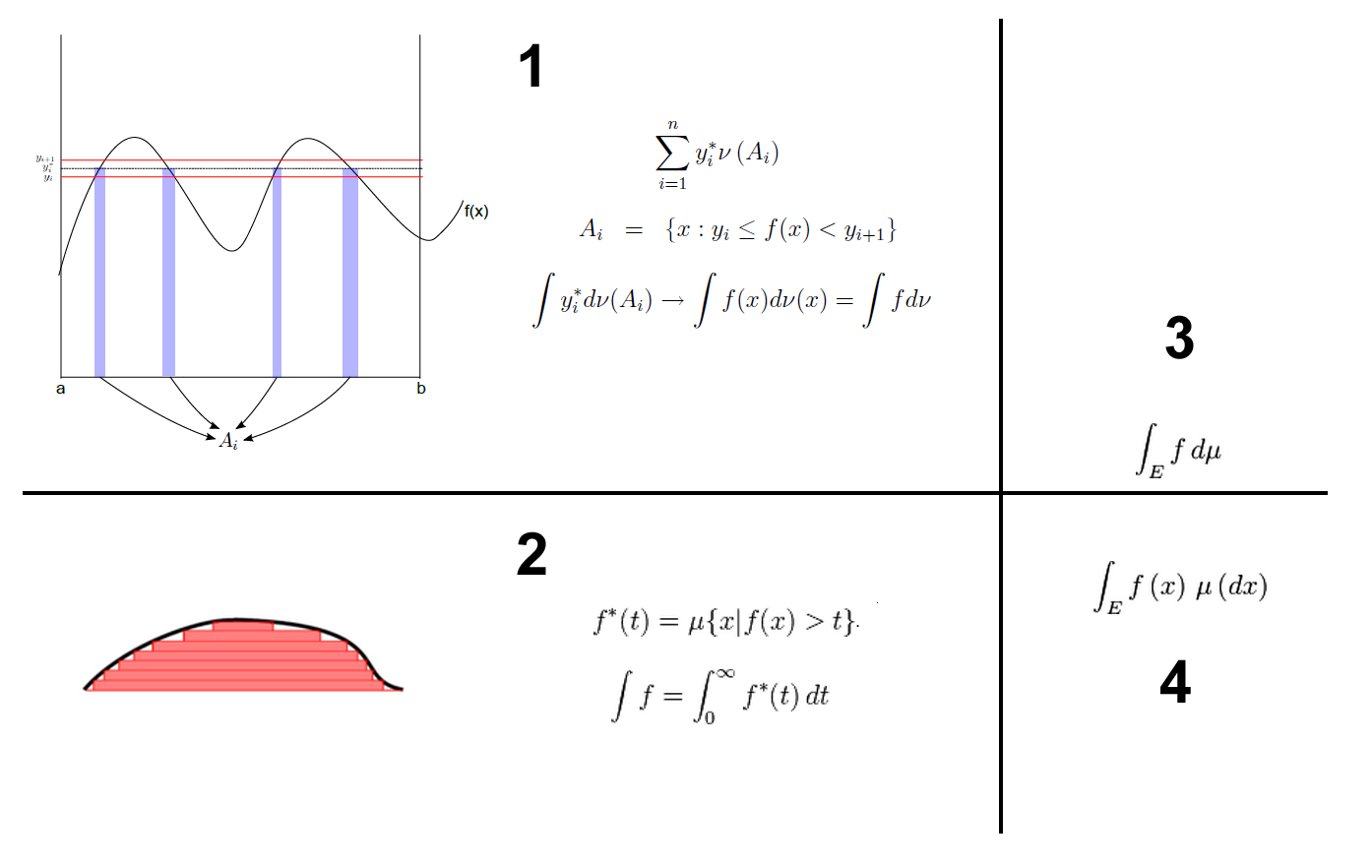
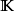
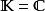
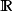
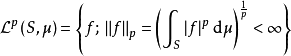

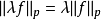



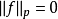
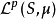

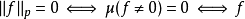
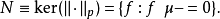
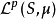
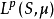
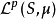
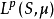
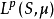

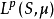


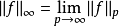

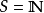

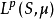
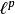
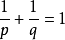
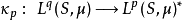
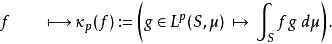
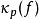
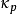
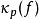
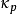
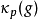
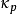
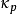
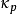

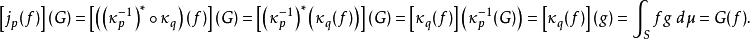
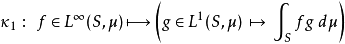
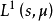
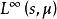
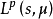
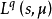

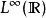
在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名,儘管依據Bourbaki (1987)...
勒貝格積分,是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是求其函式圖像與軸之間的面積。...
取R的全體子集作為F,設其σ域F',F'包括所有的區間,而且其中的元素都有測度L,且L是區間長度概念的自然推廣,可得到勒貝格測度空間(R,F',L),F'中的元素叫...
可測空間是測度的定義域,是測度論中的基本概念,在一個可測空間上可以定義不止一種測度。...
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;...
在數學裡,尤其是在泛函分析之中,巴拿赫空間是一個完備賦范向量空間。更精確地說,巴拿赫空間是一個具有範數並對此範數完備的向量空間。...
勒貝格-斯蒂爾傑斯測度簡稱(L-S)測度,是直線上勒貝格測度的推廣。勒貝格-斯蒂爾傑斯測度空間是定義了勒貝格-斯蒂爾傑斯測度的測度空間。...
縮小 F為小一點的σ域 F', 使得 F' 包括所有的區間, 而且其中的元素都有測度 L, 而且 L是區間長度概念的自然推廣, 就得到所謂勒貝格測度空間(R,F',L),...
度量空間是弗雷歇(Fréchet,M.-R.)於1906年引進的,它是現代數學中的一種基本而重要並且非常接近於歐幾里得空間的抽象空間,也是泛函分析的基礎之一。勒貝格數(...
《歐氏空間上的勒貝格積分》是2010-1出版的圖書,作者是瓊斯。...... 《歐氏空間上的勒貝格積分(修訂版)(英文版)》簡明、詳細地介紹勒貝格測度和Rn上的積分。《歐...
在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名(Dunford & Schwartz 1958,...
數學中,函式空間指的是從集合 X 到集合 Y 的給定種類的函式的集合。其叫做空間的原因是在很多套用中,它是拓撲空間或向量空間或這二者。經典分析學研究中出現了...
在數學裡,希爾伯特空間即完備的內積空間,也就是說一個帶有內積的完備向量空間。是有限維歐幾里得空間的一個推廣,使之不局限於實數的情形和有限的維數,但又不失...
勒貝格積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是函式...
勒貝格可積函式是指其勒貝格積分為有限數的函式,簡稱(L)可積函式。在(L)測度有限的集上,有界可測函式都是(L)可積函式。...
在數學中, Lp空間是由p次可積函式組成的空間;對應的lp空間是由 p次可和序列組成的空間。在泛函分析和拓撲向量空間中,他們構成了Banach空間一類重要的例子。...
勒貝格-康托爾函式是由格奧爾格·康托爾創立的,他創立了現代集合論,是實數系以至整個微積分理論體系的基礎,還提出了勢和良序概念的定義;康托爾確定了在兩個集合...
勒貝格分解定理(Lebesgue decomposition theorem)是關於σ有限廣義測度分解為絕對連續部分和奇異部分之和的重要定理,是有界變差函式的勒貝格分解定理的推廣。設(Ω,F,...
勒貝格-斯蒂爾傑斯積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看...
函式空間S又為函式空間S(E),是可測函式組成的函式類。可以在測度空間上,類似的建立S空間。...
