基本介紹
- 中文名:半範數
- 外文名:seminorm
- 實質:非負實值函式
- 相關概念:均衡吸收凸子集,Minkowski泛函
- 聯繫:局部凸空間
- 套用領域:拓撲線性空間理論
定義





相關概念








































局部凸空間




























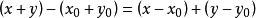






























































































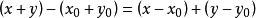





















半範數(seminorm)是範數的一種推廣,其比範數的要求弱(半範數比範數少一個條件:使半範數值為0的元素不一定是0元素),範數一定是半範數。局部凸線性空間的拓撲...
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
設E是局部凸空間,如果E的拓撲可由可列個連續半範數{pn(∙)}確定,則稱E是賦可列半范線性空間。...
二範數指矩陣A的2範數,就是A的轉置共軛矩陣與矩陣A的積的最大特徵根的平方根值,是指空間上兩個向量矩陣的直線距離。類似於求棋盤上兩點間的直線距離。...
BMO範數(BMO norm)記為||f||∗,其中,BMO是有界平均振動之意。...... BMO範數(BMO norm)記為||f||∗,其中...半範數可以為非零的矢量賦予零長度。...
在數學中,賦范向量空間是具有“長度”概念的向量空間。是通常的歐幾里德空間Rn的推廣。Rn中的長度被更抽象的範數替代。“長度”概念的特徵是:零向量的長度是零,...
一個半賦范向量空間(E,p)由一個向量空間E以及一個E上的半範數p構成。一個賦范向量空間(E,||·||)由一個向量空間E以及一個E上的範數||·|| 構成。 [...
一個把向量映射到非負實數的函式如果滿足簡介中描述的性質,就叫做一個半範數;如果只有零向量的函式值是零,那么叫做範數。擁有一個範數的向量空間叫做賦范向量空間,...
弱拓撲(weak topology)是一種局部凸拓撲。設線性空間對(X,Y)關於雙線性泛函〈·,·〉成為對偶,稱X上由半範數族{|〈·,y〉||y∈Y}確定的局部凸拓撲為X的...
強運算元拓撲(strong operator topology)是運算元空間中的又一種拓撲。從賦范線性空間X到賦范線性空間Y的有界線性運算元全體所成的賦范線性空間B(X→Y)中由半范族{...
E成為桶型空間的充分必要條件是每個下半連續的半範數必是連續的。桶型空間的研究與一致有界定理在拓撲線性空間中的推廣有密切的聯繫。 [1] ...
由半範數族{pA(x)|A∈𝒴}確定的X上局部凸拓撲T𝒴,稱為關於對偶線性空間(X,Y)的一個可允許拓撲,而相應的有界集族𝒴稱為可允許集族。...
是一個半範數,取幾乎處處為0,則關於的商空間是一個賦范向量空間,記作。一致範數與p-範數之間存在以下關係:可以證明,L空間是完備的空間,也即是說是一個巴拿赫空...
次線性函式(sublinear function)是一類重要的凸函式。正齊次且是次可加的函式稱為次線性函式。局部凸空間(包括賦范線性空間、有限維空間)上的下半連續次線性函式...
為局部凸空間且 為其局部基,X是Hausdorff空間若且唯若 有 ,稱 為由半範數族 生成的拓撲。 [2] 局部有界空間推論1 賦范空間是Hausdorff的局部凸空間。局部...
則由半範數族{pA(x)|A∈𝒴}確定的X上局部凸拓撲T𝒴,稱為關於對偶線性空間(X,Y)的一個可允許拓撲,或在集類𝒴上的一致收斂拓撲,而相應的有界集族𝒴...
有界型空間是擬桶型的,但不一定是桶型的,桶型空間也不一定是有界型的,可度量化局部凸空間,即其拓撲由至多可數個半範數所確定的空間,是有界型空間。完備的...
強拓撲是一種拓撲。局部凸空間X中原有的拓撲,相對於弱拓撲σ(X,X)稱為X的強拓撲。例如賦范線性空間的強拓撲即為範數拓撲。部凸空間是最重要的一類拓撲線性空間...
