可允許拓撲是一種局部凸拓撲,也可稱為集類𝒴上的一致收斂拓撲,而相應的有界集族𝒴稱為可允許集族。
基本介紹
- 中文名:可允許拓撲
- 外文名:admissible topology
- 適用範圍:數理科學
簡介
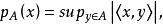
局部凸拓撲
半範數


可允許拓撲是一種局部凸拓撲,也可稱為集類𝒴上的一致收斂拓撲,而相應的有界集族𝒴稱為可允許集族。
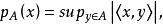


可允許拓撲是一種局部凸拓撲,也可稱為集類𝒴上的一致收斂拓撲,而相應的有界集族𝒴稱為可允許集族。...
由半範數族{pA(x)|A∈𝒴}確定的X上局部凸拓撲T𝒴,稱為關於對偶線性空間(X,Y)的一個可允許拓撲,而相應的有界集族𝒴稱為可允許集族。...
當匯流排負載不允許時還可以擴充匯流排;使用的電纜少,且安裝容易;使用的設備相對簡單...匯流排拓撲的優缺點是:優點是結構簡單,可擴充性好。缺點是維護難、單點的結構...
這種網路拓撲結構是由星型結構和匯流排型結構的網路結合在一起的網路結構,這樣的拓撲結構更能滿足較大網路的拓展,解決星型網路在傳輸距離上的局限,而同時又解決了...
拓撲可測空間是帶有拓撲結構的可測空間。設τ是Ω上的拓撲,σ(r)是由τ生成的σ代數,稱(Ω,τ,σ(r))為一個拓撲可測空間。...
可賦范拓撲線性空間(normable topological linear space)是指可用範數來刻畫拓撲的拓撲線性空間。...
對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是將G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊∈E(G),則u線上性序列中...
商拓撲可以被如下地定義出來:若X是一個拓撲空間,Y是一個集合,如果f:X→Y是一個滿射,那么Y獲得一個拓撲;該拓撲的開集可如此定義,一個集合是開的,若且唯若...
拓撲群又名連續群,是具有拓撲空間結構的群。在數學中,拓撲群是群 G 和與之一起的 G 上的拓撲,使得這個群的二元運算和這個群的取逆函式是連續的。拓撲群允許...
拓撲絕緣體是一種內部絕緣,界面允許電荷移動的材料。在拓撲絕緣體的內部,電子能帶結構和常規的絕緣體相似,其費米能級位於導帶和價帶之間。在拓撲絕緣體的表面存在...
計算機網路拓撲(Computer Network Topology)是指由計算機組成的網路之間設備的分布情況以及連線狀態.把它兩畫在圖上就成了拓樸圖.一般在圖上要標明設備所處的位置,...
有中心拓撲結構是WLAN的基本結構,至少包含一個AP作為中心站構成星形結構。在AP覆蓋範圍內的所有站點之間的通信和接入網際網路均由AP控制,AP與有線乙太網中的Hub類似...
拓撲流形定向確定流形指向的方式問題.有多種等價的方式來定義流形的定向.這裡介紹比較基本的兩種.設M為n維拓撲流形。拓撲流形定向[1] (orientation of ...
在數學中,同倫(Homotopy)的概念在拓撲上描述了兩個對象間的“連續變化”。 [1] 兩個拓撲空間如果可以通過一系列連續的形變從一個變到另一個,那么就稱這兩...
麥基空間(Mackey space)是一類局部凸空間。設(X,Y)為對偶線性空間,在Y的每個弱緊凸集上一致收斂的拓撲是一種可允許拓撲,稱為X上的麥基拓撲,記為τ(X,Y)。...
幾何拓撲學是十九世紀形成的一門數學分支,它屬於幾何學的範疇。有關拓撲學的一些內容早在十八世紀就出現了。那時候發現一些孤立的問題,後來在拓撲學的形成中占著...
