基本介紹
- 中文名:拓撲群
- 外文名:Topological group
- 又名:連續群
- 簡介:是具有拓撲空間結構的群
- 套用學科:數學
- 相關術語:群
形式定義
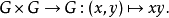


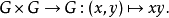

拓撲群又名連續群,是具有拓撲空間結構的群。在數學中,拓撲群是群 G 和與之一起的 G 上的拓撲,使得這個群的二元運算和這個群的取逆函式是連續的。拓撲群允許...
模糊拓撲群是具有拓撲空間結構的群,其中模糊鄰域系是研究模糊拓撲群的基本工具。其最大的特徵擁有相應的拓撲空間。...
《拓撲群引論》是1999年科學出版社出版的圖書,作者是黎景輝、馮緒寧。...... 本書介紹了拓撲群的基本概念、測度與積分、拓撲群(特別是緊、局部緊的拓撲群)的表示...
拓撲子群(topological subgroup)類似於群論中的子群.設G為拓撲群,H是G作為抽象群的子群,H又可視為拓撲空間G的子空間,從而可在H中引人誘導拓撲.於是,H相對於...
拓撲空間是一種數學結構,可以在上頭形式化地定義出如收斂、連通、連續等概念。拓撲空間在現代數學的各個分支都有套用,是一個居於中心地位的、統一性的概念。拓撲...
代數拓撲(Algebraic topology)是使用抽象代數的工具來研究拓撲空間的數學分支。賦以拓撲的集合叫拓撲空間。拓撲基[topologique (base)]設E為拓撲向量空間,則E的任一...
拓撲同構(topological isomorphism)拓撲群之間的同構概念.設G G:都是拓撲群,若筍:G,~GZ是群同構,而且筍和抓‘都是連續函式,則稱筍是拓撲同構,稱兩個群G,和...
拓撲域(topological field)是具有拓撲結構的域。若F是一個域,同時為一個拓撲空間,而且F中的代數運算在拓撲空間F中是連續的。拓撲空間是歐幾里得空間的一種推廣。...
拓撲流形,為最容易定義的流形,它局部看起來象一些“普通”的歐氏空間Rn。形式化的講,一個拓撲流形是一個局部同胚於一個歐氏空間(或上半歐式空間)的拓撲空間。...
一般拓撲學(geoneral topology)是用點集的方法研究拓撲不變數的拓撲分支。它的前身是點集拓撲學。 一般拓撲學的歷史約六十年,由於它適應了科學的發展,其生命力是...
克魯爾拓撲(Krull topology)是一種拓撲。用以推廣有限伽羅瓦理論的基本定理。它是克魯爾(Krull,W.)於1928年對無限伽羅瓦群引入的。...
離散群是配備了離散拓撲的群G。帶有這種拓撲 G成為了拓撲群。拓撲群 G的離散子群是其相對拓撲為離散拓撲的子群H。...
無限群指元素個數為無限的群。拓撲群,李群,(無限)典型群,代數群,算術群,都是無限群。無限群的研究開始於19世紀下半葉。正當抽象群的概念形成之際,數學家們...
群上調和分析又稱群上傅立葉分析、抽象調和分析。它是古典調和分析(即傅立葉級數與傅立葉積分理論)的統一與推廣。它的研究對象是拓撲群上的函式或測度以及由它們...
20世紀30年代末,他研究了拓撲群上的積分問題,並於1940年完成了專著《拓撲群上的積分及其套用》。這本書反映出的數學結構主義體現了布爾巴基學派的觀點,開闢了群...
