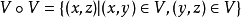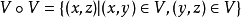一致空間
在一致結構和拓撲結構之間的概念區別是在一致空間內可以形式化有關於相對鄰近性和點間臨近性的特定概念。換句話說,想法如“
x鄰近於
a勝過
y鄰近於
b”在一致空間是有意義的。相對的,在一般
拓撲空間內,給定集合
A, B只能有意義的說點
x“任意鄰近”
A(就是說在 A 的
閉包中),或者說
A是比
B更小的
x的“
鄰域”,但是點間鄰近性和相對鄰近性不能單獨用拓撲結構描述。
一致結構
一致結構是集合上的一種結構。設X為集合,U為X×X的非空
子集族。若U滿足下列條件,則稱U是X上的一致結構:
1.U的每一個元包含對角線Δ.
2.若U∈U,則U^-1∈U,其中:
U^-1={(x,y)|(y,x)∈U}.
5.若U∈U並且UVX×X,則V∈U.
具有一致結構U的集合X稱為一致空間,記為(X,U)。一致空間的概念是
韋伊(Weil,A.)於1938年引入的。
布爾巴基(Bourbaki,N.)於1940年首先給予系統的論述。圖基(Tukey,J.W.)於1940年用覆蓋族定義並研究了一致空間的等價的概念。艾斯貝爾(Isbell,J.R.)於1964年出版的書中,包含了用覆蓋敘述的一致空間理論的重要發展.一致空間也可用偽度量族來描述,它是由布爾巴基於1948年給出的。
定義
一致空間有三個等價定義。
周圍定義
一致空間(
X, Φ) 是
集合X配備了
笛卡爾積X×
X的非空
子集族(Φ 叫做
X的
一致結構或
一致性而它的元素叫做
周圍(
法語entourage:鄰居或周圍))滿足如下公理:
如果 U在 Φ 中,則 U包含對角 Δ = { (x, x) : x∈ X}。
如果 U在 Φ 中而 V是包含 U的 X× X的子集,則 V在 Φ 中。
如果 U和 V在 Φ 中,則 U∩ V在 Φ 中。
如果 U在 Φ 中,則存在 V在 Φ 中,使得只要 (x, y) 和 (y, z) 在 V中,則 (x, z) 在 U中。
如果 U在 Φ 中,則 U= { (y, x) : (x, y) ∈U} 也在 Φ 中。
如果省略了最後的性質則稱空間為
準一致的。注意二三兩條是
濾子的定義。
通常寫 U[x]={y : (x,y)∈U}。在圖形上,典型的周圍被繪製為圍繞“y=x”對角的斑點;U[x] 們則為縱截面。如果 (x,y) ∈ U,則可以說 x和 y是“U-鄰近”的。類似的,如果在 X的子集 A中的所有成對的點都是 U-鄰近的(就是說如果 A× A被包含在 U中),則 A被稱為“U-小”的。周圍 U是對稱的,如果 (y,x) ∈ U正好在 (x,y) ∈ U的時候。第一個公理聲稱對於每個周圍 U每個點都是 U-鄰近於自身。第三個公理保證“同時 U-鄰近和 V-鄰近二者”也是在一致性中的鄰近關係。第四個公理聲稱對於每個周圍 U都有一個周圍 V是“一半大”的。最後的公理聲稱“鄰近”關於一致結構的本質對稱性質。
一致性 Φ 的基礎周圍系統是 Φ 的周圍的任何集合 B,使得所有 Ф 的周圍包含屬於 B的一個集合。因此,通常上述性質 2,基礎周圍系統 B足夠無歧義的指定一致 Φ: Φ 是包含 B的一個集合的 X× X的子集的集合。所有一致空間都用由對稱周圍構成的基礎周圍系統。
關於一致性的正確直覺可由
度量空間的實例提供:如果 (
X,
d) 是度量空間,集合
這裡的
形成了 X的標準一致結構的基礎周圍系統。則 x和 y是 Ua-鄰近的,正好在 x與 y之間距離最多為 a的時候。
一致性 Φ “精細”於在同一個集合上的另一個一致性 Ψ,如果 Φ ⊇ Ψ;此時 Ψ 被稱為“粗糙”於 Φ。
偽度量定義
一致空間可以使用
偽度量系統來等價的定義,這是對
泛函分析(帶有
半範數提供的偽度量)特別有用的方式。更精確地說,設
f:
X×
X→
R是在集合
X上的偽度量。逆像
Ua=
f([0,a])對於
a> 0 可以被證實形成了一致的基礎周圍系統。由
Ua生成的一致是由單一的偽度量
f所定義的一致。
對於在 X上的偽度量族 (fi),這個族所定義的一致結構是單獨偽度量 fi所定義的一致結構的“最小上界”。這個一致性的基礎周圍系統由單獨偽度量 fi所定義的一直的周圍的有限交集的集合來提供。如果偽度量的族是有限的,可以看出同樣的一致結構可以定義自單一的偽度量,就是這個族的“上包絡” sup fi。
更少瑣碎的,可證實允許可數的基礎周圍系統(並因此特別為由可數的偽度量族定義的一致)可以定義自一個單一偽度量。結論是任何一致結構都可以如上述那樣的定義自(可能不可數)偽度量族(參見 Bourbaki:《General Topology》 Chapter IX §1 no. 4)。
一致覆蓋定義
一致空間(
X,
Θ) 是集合
X配備顯著的“一致覆蓋”族
Θ,它來自
X的覆蓋的集合,在按星號精緻排序的時候形成了
濾子。你可以稱呼覆蓋
P是覆蓋
Q的
星號精緻(refinement)寫為
P<*
Q,如果對於所有
A∈
P,有
U∈
Q使得如果
A∩
B≠∅,
B∈
P,則
B⊆
U。公理化可簡約為:
{X} 是一致覆蓋。
如果 P<*Q並且 P是一致覆蓋,則 Q也是一致覆蓋。
如果 P並且 Q是一致覆蓋,則有一致覆蓋 R精緻 P和 Q二者。
給定一個點
x和一致覆蓋
P,可以把包含
x的
P的成員的
並集認為是
x的大小
P的典型
鄰域,並且這個直覺度量一致的適用在這個空間之上。
給定在周圍意義上的一個一致空間,定義覆蓋 P為一致的,如果存在某個周圍 U使得對於每個 x∈X,有一個 A∈P使得 U[x]⊆A。這些一致覆蓋形成了第二種定義的一致空間。反過來說,給定在一致覆蓋意義上的一個一致空間, ∪{A×A : A∈P} 的超集,因為 P取值於一致覆蓋上,是第一種定義的一致空間的周圍。此外,這兩個變換是互逆的。
拓撲
定義
所有一致空間
X都可以變成
拓撲空間,通過定義
X的子集
O為開集,若且唯若對於所有
O中的
x存在周圍
V使得
V[
x] 是
O的子集。在這個
拓撲中,點
x的
鄰域濾子是 {
V[
x]:V∈Φ}。這可以通過
遞歸的使用“一半大”周圍的存在性來證明。相較於一般拓撲空間,一致結構的存在性使得比較鄰域大小成為可能:
V[
x] 和
V[
y] 被認為是“一樣大”。
一致結構所定義的拓撲被稱為引發自一致性。在拓撲空間上一致結構兼容於這個拓撲,如果這個一致結構定義的拓撲同最初的拓撲相符合。一般的說有多個不同的一致結構可以兼容於在 X上的給定拓撲。
可一致化空間
拓撲空間被稱為
可一致化的,如果一致結構兼容於這個拓撲。
所有可一致化空間是完全正則拓撲空間。此外,對於可一致化空間 X下列等價:
對於任何兼容的一致結構,所有周圍的交集是對角 {(x, x) : x∈ X}。
可一致化空間的拓撲總是對稱拓撲;就是說這個空間是 R0空間。
反過來說,每個完全正則空間都是可一致化的。兼容於完全正則空間
X的
拓撲的一個一致性可以定義為最粗糙一致性,它使得所有
X上的連續實數值函式為
一致連續。這個一致性的基礎周圍系統提供為集合 (
f×
f)(
V) 的所有有限交集,這裡的
f是
X上的連續實數值函式而
V是一致空間
R的周圍。這個一致性定義了一個拓撲,它明顯的粗糙於
X的最初拓撲;並且它還精細於最初的拓撲(因此與它相符合)是完全
正則性的簡單推論:對於任何
x∈
X和
x的
鄰域 V,有連續實數值函式
f有著
f(
x)=0 並對於
V的
補集中的點等於 1。
特別是,緊緻
豪斯多夫空間是可一致化的。事實上,對於緊緻豪斯多夫空間
X在
X×
X中對角的所有鄰域的集合形成了唯一的兼容於這個
拓撲的一致性。
豪斯多夫一致空間是可度量空間,如果它的一致性可以定義自為可數的偽度量族。實際上,如在上面偽度量定義中討論的,這種一致性可以定義自單一的偽度量,如果這個空間是豪斯多夫的,則它必然是度量。特別是,如果
矢量空間的拓撲是豪斯多夫的並且可定義自可數的
半範數族,則它是可度量的。
一致連續
一致連續函式被定義為其周圍的逆像還是周圍的函式,或等價的說,一致覆蓋的逆像還是一致覆蓋的函式。
完備性
在一致空間
X上的
柯西濾子F是濾子
F使得對於所有周圍
U,存在
A∈
F有著
A×
A⊆
U。換句話說,一個濾子是柯西濾子,如果它包含“任意小”集合。可從定義中得出每個(關於這個一直結構定義的
拓撲)收斂的濾子都是柯西濾子。柯西濾子叫做“極小”的,如果不包含更小(就是更粗)的柯西濾子(除了自己)。可以證明所有柯西濾子包含一個唯一的“極小柯西
濾子”。每個點的
鄰域濾子(由這個點的所有鄰域構成的濾子)是極小柯西濾子。
反過來說,一致空間稱為
完備的,如果所有柯西濾子收斂。任何緊緻
豪斯多夫空間都是關於兼容於這個拓撲的一致結構的完備一致空間。
完備一致空間享有如下重要性質:如果
f:
A→
Y是從一致空間
X的稠密子集
A到完備一致空間
Y的
一致連續函式,則
f可以擴張(唯一的)成在整體
X上的一致連續函式。
一致空間的豪斯多夫完全
如同
度量空間,所有一致空間
X都
豪斯多夫完全:就是說存在一個完備豪斯多夫一致空間
Y和
一致連續映射
i:
X→
Y帶有如下性質:
對於任何從 X到完備豪斯多夫一致空間 Z的一致連續映射 f,存在一個唯一的一致連續映射 g: Y→ Z使得 f= gi。
豪斯多夫完全
Y是唯一的上至
同構。作為一個集合
Y可以選取為由
X上的極
小柯西
濾子組成。作為每個
X中點
x的
鄰域濾子
B(
x),映射
i可以被定義為把
x映射到
B(
x)。如此定義的映射
i一般不是
單射;事實上,等價關係
i(
x) =
i(
x') 的圖象是
X的所有周圍的交集,因此
i是單射正好在
X是
豪斯多夫空間的時候。
在
Y上的一致結構定義如下:對於每個對稱周圍
V(就是說使得 (
x,
y) 在
V中正好在 (
y,
x) 在
V的時候),設
C(
V) 是“至少共有一個 V-小集合”的所有極小柯西
濾子的對 (
F,
G) 的集合。集合
C(
V) 可以被證實形成了基礎周圍系統;如此就定義了配備了這個一致結構的
Y。
集合
i(
X) 因此是
Y的稠密子集。如果
X是
豪斯多夫空間,則
i是到
i(
X) 的
同構,因此
X可用它的完全的稠密子集來識別。此外,
i(
X) 總是
豪斯多夫的;它叫做關聯於
X的
豪斯多夫一致空間。如果
R指示等價關係
i(
x) =
i(
x'),則
商空間 X/
R同胚於
i(
X)。
例子
所有
度量空間(
M,
d) 都可被當作一致空間。實際上因為度量是當然的偽度量,上文的偽度量定義給出了
M的一致結構。這個一致性的基礎周圍系統提供自集合 。這個
M的一致結構生成了在
M上的正常度量空間
拓撲。但是,不同的度量空間可以有相同的一致結構(平凡的例子可通過度量的常數提供)。這個一致結構還生成
一致連續和度量空間的完備性的等價定義。
使用度量,可以構造有相符合拓撲的不同一致結構的簡單例子。例如,設
d1(
x,
y) = |
x − y| 是在
R上的正常度量,並設
d2(
x,
y) = |
e− e|。則這兩個度量都引發在
R上的正常
拓撲,但是一致結構是不同的,因為 { (x,y) : | x − y | < 1 } 是
d1的一致結構的周圍但不是
d2的。非正式的,這個例子可以被看作選取正常的一致性並通過連續但非
一致連續函式的作用扭曲它。
所有
拓撲群G(特別是所有拓撲矢量空間)成為一致空間,如果我們定義
G×
G的子集
V是周圍,若且唯若它包含集合 { (
x,
y) :
x⋅
y∈
U} 對於
G的
單位元的某個
鄰域U。這個
G上的一致結構叫做在
G上的右一致性,因為對於所有
G中的
a,右乘法
x→
x⋅
a是關於這個一致結構
一致連續的。你還可以定義
G上的左一致性;它們兩個不需要相符合,但是它們都生成在
G上的給定
拓撲。
歷史