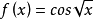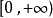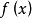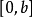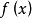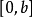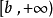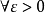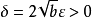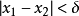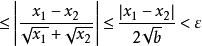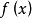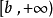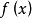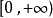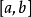某一函式f在區間I上有定義,如果對於任意的ε>0,總有δ>0 ,使得在區間I上的任意兩點x'和x",當滿足|x'-x"|<δ時,|f(x')-f(x")|<ε恆成立,則該函式在區間I上一致連續。對於在閉區間上的連續函式,其在該區間上必一致連續。一致連續的函式必定是連續函式。
基本介紹
- 中文名:一致連續
- 外文名:Uniform Continuity
- 所屬學科:高等數學
- 特點:一致連續的連續性比連續更強
- Cantor定理:f在[a,b]連續則在該區間一致連續
- 性質:一致連續的函式必定是連續函式
定義
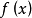
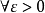
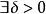

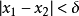
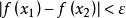
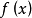
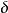


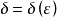
意義
定理
定理1 Cantor定理或一致連續性定理
定理2

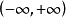

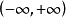
定理3
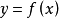
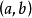
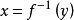

定理4


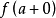



定理5
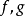
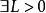
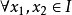
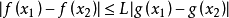
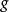
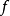
性質
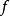
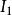
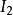

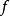
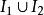

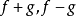
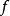
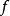




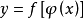
舉例