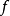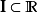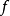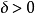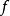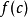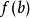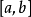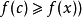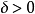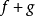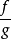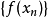連續(數學名詞)

在數學中，連續是函式的一種屬性。直觀上來說，連續的函式就是當輸入值的變化足夠小的時候，輸出的變化也會隨之足夠小的函式。如果輸入值的某種微小的變化會產生輸出值的一個突然的跳躍甚至無法定義，則這個函式被稱為是不連續的函式（或者說具有不連續性）。

常用的連續性的最根本定義是在拓撲學中的定義，在條目連續函式 (拓撲學)中會有詳細論述。在序理論特別是域理論中，有從這個基礎概念中得出的另一種抽象的連續性：斯科特連續性。

基本介紹

• 中文名：連續
• 外文名：Continuity
• 最早出現：數學分析
• 推廣：點集拓撲

實值連續函式

最基本也是最常見的連續函式是定義域為實數集的某個子集、取值也是實數的連續函式。例如前面提到的花的高度，就是屬於這一類型。這類函式的連續性可以用直角坐標系中的圖像來表示。一個這樣的函式是連續的，如果粗略地說，它的圖像為一個單一的不破的曲線，並且沒有間斷、跳躍或無限逼近的振盪。

嚴格來說，設 是一個從實數集的子集 射到 的函式： 。 在 中的某個點 處是連續的若且唯若以下的兩個條件滿足：

1. 在點 上有定義。

2. 是 中的一個聚點，並且無論自變數 在 中以什麼方式接近 ， 的極限都存在且等於 。

我們稱函式到處連續或處處連續，或者簡單的稱為連續，如果它在其定義域中的任意一點處都連續。更一般地，當一個函式在定義域中的某個子集的每一點處都連續時，就說這個函式在這個子集上是連續的。

定義

不用極限的概念，也可以用下面所謂的 方法來定義實值函式的連續性。

仍然考慮函式 。假設 是 的定義域中的元素。函式 被稱為是在 點連續若且唯若以下條件成立：

對於任意的正實數 ，存在一個正實數 使得對於任意定義域中的 ，只要 滿足 ，就有 成立。

連續性的“ 定義”由柯西首先給出。

更直觀地，函式 是連續的若且唯若任意取一個 中的點 的鄰域 ，都可以在其定義域 中選取點 的足夠小的鄰域，使得 的鄰域在函式 上的映射下都會落在 的鄰域 之內。

以上是針對單變數函式（定義域在 上的函式）的定義，這個定義在推廣到多變數函式時也是成立的。度量空間以及拓撲空間之間的連續函式定義見下一節。

例子

• 所有多項式函式都是連續的。各類初等函式，如指數函式、對數函式、平方根函式與三角函式在它們的定義域上也是連續的函式。
• 絕對值函式也是連續的。
• 定義在非零實數上的倒數函式f= 1/x是連續的。但是如果函式的定義域擴張到全體實數，那么無論函式在零點取任何值，擴張後的函式都不是連續的。
• 非連續函式的一個例子是分段定義的函式。例如定義f為：f(x) = 1如果x> 0，f(x) = 0如果x≤ 0。取ε = 1/2，不存在x=0的δ-鄰域使所有f(x)的值在f(0)的ε鄰域內。直覺上我們可以將這種不連續點看做函式值的突然跳躍。
• 另一個不連續函式的例子為符號函式。

連續函式的性質

如果兩個函式f和g是連續的， 為一個實數，那么 、 和 都是連續的。所有連續函式的集合構成一個環，也構成一個向量空間（實際上構成一個代數）。如果對於定義域內的所有 ，都有 ，那么 也是連續的。兩個連續函式的複合函式 也是連續函式。

如果實函式f在閉區間內連續，且 是某個 和 之間的數，那么存在某個 內的 ，使得，這個定理稱為介值定理。例如，如果一個小孩在五歲到十歲之間身高從1米增長到了1.5米，那么期間一定有某一個時刻的身高正好是1.3米。

如果f在 內連續，且 和一正一負，則中間一定有某一個點 ，使得 。這是介值定理的一個推論。

如果f在閉區間 內連續，則它一定取得最大值，也就是說，總存在 ，使得對於所有的 ，有 。同樣地，函式也一定有最小值。這個定理稱為極值定理。（注意如果函式是定義在開區間 內，則它不一定有最大值和最小值，例如定義在開區間(0,1)內的函式 。）

如果一個函式在定義域中的某個點 可微，則它一定在點 連續。反過來不成立；連續的函式不一定可微。例如，絕對值函式在點 連續，但不可微。

度量空間之間的連續函式

現在考慮從度量空間 到另一個度量空間 的函式 。

在 是連續的，則對任何實數 ，存在一個實數 使得 ，只要滿足 ，就滿足 。

這個定義可以用序列與極限的語言重述：

如果函式 在點 連續，則對 中任何序列 ，只要 ，就有 。連續函式將極限變成極限。

後一個條件可以減弱為：

在 點連續，若且唯若對 中任何序列 ，只要 ，就滿足序列 是一個柯西序列。連續函式將收斂序列變成柯西序列。

拓撲空間之間的連續函式

如上連續函式的定義可以自然地推廣到一個拓撲空間到另一拓撲空間的函式：函式 ，這裡 與 是拓撲空間是連續的若且唯若任何開集的逆像是 中的開集。

相關條目

• 單一連續
• 一致連續
• 有界線性運算元
• 絕對連續
• 半連續