初等函式

初等函式是由冪函式（power function）、指數函式（exponential function）、對數函式（logarithmic function）、三角函式（trigonometric function）、反三角函式（inverse trigonometric function）與常數經過有限次的有理運算（加、減、乘、除、有理數次乘方、有理數次開方）及有限次函式複合所產生，並且能用一個解析式表示的函式。

基本介紹

• 中文名：初等函式
• 外文名：elementary function
• 分類：代數函式和超越函式
• 作用：研究函式的一般理論中起重要作用
• 非初等函式：狄利克雷函式和黎曼函式等
• 套用領域：高等數學、數學分析等

概念

初等函式

初等函式是由冪函式（power function）、指數函式（exponential function）、對數函式（logarithmic function）、三角函式（trigonometric function）、反三角函式（inverse trigonometric function）與常數經過有限次的有理運算（加、減、乘、除、有理數次乘方、有理數次開方）及有限次函式複合所產生，並且能用一個解析式表示的函式。

它是最常用的一類函式，包括常函式、冪函式、指數函式、對數函式、三角函式、反三角函式（以上是基本初等函式），以及由這些函式經過有限次四則運算或函式的複合而得的所有函式。即基本初等函式經過有限次的四則運算或有限次的函式複合所構成並可以用一個解析式表出的函式，稱為初等函式。

還有一系列雙曲函式也是初等函式，如sinh的名稱是雙曲正弦或超正弦，cosh是雙曲餘弦或超餘弦，tanh是雙曲正切，coth是雙曲餘切，sech是雙曲正割，csch是雙曲餘割。初等函式在其定義區間內一定連續。

一個初等函式，除了可以用初等解析式表示以外，往往還有其他表示形式。例如 ，三角函式 y=sinx 可以用無窮級數表為y=x-x³/3!+x⁵/5!-…初等函式是最先被研究的一類函式，它與人類的生產和生活密切相關，並且套用廣泛。為了方便，人們編制了各種函式表，如平方表、開方表、對數表、三角函式表等。

有理函式

實係數多項式稱為整有理函式。其中最簡單的是線性函式 y=α₀+α₁x，它的圖象是過y軸上y=α₀點的斜率為α₁的直線。二次整有理函式y=α₀+α₁x+α₂x²的圖象為拋物線。

兩個整有理函式之比為分式有理函式。分式有理函式其中最簡單的是反比例函式，其圖象為雙曲線。整有理函式和分式有理函式統稱有理函式。有理函式起源於代數學。

兩個復係數的多項式之比為有理函式，它實現擴充的複平面到自身的解析映射。分式線性函式是一個特殊的有理函式，它在複分析中有重要的意義。另一個特殊情形是冪函式w=zⁿ，n 是自然數，它在全平面是解析的。因此當n≥2時，它在全平面除z=0以外到處實現共形映射（保角映射）。它將圓周|z|= r變為圓周|w|=rn，將射線argz=θ變為射線argw=nθ。任何一個區域,只要該區域中任兩點的輻角差小於2π/n，它就是w=zⁿ的單葉性區域。冪函式w=zⁿ的反函式為根式函式，它有n個值(k=0，1，…，n-1)，稱為它的分支。它們在任何區域θ₁z<θ₁+2π中都單值解析。

代數函式

求有理函式的反函式則可產生代數函式。如y=xⁿ的反函式為x=yⁿ。

超越函式

超越函式指變數之間的關係不能用有限次加、減、乘、除、乘方、開方運算表示的函式。如指數函式、對數函式、反三角函式等就屬於超越函式。

常用函式

常函式

對定義域中的一切x對應的函式值都取某個固定常數的函式。

常函式

三角函式

三角函式是起源於幾何學的最簡單的超越函式。

初等三角函式包括正弦函式y=sinx 、餘弦函式y=cosx 、正切函式y=tanx、餘切函式y=cotx 、正割函式y=secx和餘割函式y=cscx。高等分析學中用弧度制計量角度，即以單位圓周上的弧段量度相應的圓心角。

指數函式

形如 的函式，式中a為不等於1的正常數。

指數函式

對數函式

指數函式的反函式，記作 ，式中a為不等於1的正常數，定義域是零到正無窮的開區間。指數函式與對數函式之間成立關係式， 。

反三角函式

三角函式的反函式 ——反正弦函式y = arcsinx 、反餘弦函式 y=arccosx （－1≤x≤1，0≤y≤π）、反正切函式y=arctanx 、反餘切函式 等 ， 以上這些函式常統稱為基本初等函式。

雙曲函式

由指數函式經有理運算可導出雙曲函式。其性質與三角函式很相似。sinhx、coshx分別稱為雙曲正弦和雙曲餘弦。像三角函式一樣，由它們導出的雙曲正切tanhx=sinhx/coshx和雙曲餘切cothx=coshx/sinhx等都稱為雙曲函式。

雙曲正弦或超正弦

雙曲餘弦或超餘弦

雙曲正切

雙曲餘切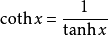

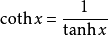
雙曲正割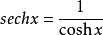

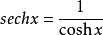
雙曲餘割

它們有如下的幾何解釋，即雙曲線x²-y²=1(x>0)上取一點M，又令O為原點，N=(1,0)，將ON，OM和雙曲線上的弧所圍面積記為θ/2，點M的坐標視為θ的函式，並記為coshθ和sinhθ，即有表示式cosh²θ-sinh²θ=1。

冪函式

形如 的函式，式中a為實常數。

部分冪函式圖像

一般地，形如 （a為常數）的函式，即以底數為自變數，冪為因變數，指數為常量的函式稱為冪函式。例如函式y=x、y=x²、y=1/x（註：y=1/x=x^-1）等都是冪函式。

在複數域的推廣

復變三角函式

例如將y=sinx和y=cosx中變數x換為復變數z，則得到復變三角函式w=sinz和w=cosz，它們是整函式。tanz=sinz/cosz，cotz=cosz/sinz等是z的亞純函式。它們具有實三角函式的很多類似性質：周期性、微商性質、三角恆等式等。但|sinz|≤1，|cosz|≤1不是對任何z都成立。三角函式與指數函式密切聯繫，因此套用時很方便。sinz的單葉性區域將Gk單葉並共形地映為全平面上除去實軸上線段[-1，1]和負虛軸後得到的區域；它將Rk單葉並共形地映為全平面除去實軸上兩條射線( ,-1]和[1, )後得到的區域。類似地可以指出cosz的單葉性區域。

復變指數函式

在指數函式式w=e^x中將x換為復變數z，便得到復變指數函式w=e^z。復變指數函式有類似於實指數函式的性質：e^z是一整函式且對任何複數z，e^z≠0；它滿足e^z1·e^z2=e^z1+z2；e^z以2kπi為周期，e^z=e^z+2kπi；並且它的導數與本身相同，即 (e^z)'=e^z。函式w=e^z在全平面實現共形映射。任何一個區域，只要對區域內任兩點，其虛部之差小於2π，它就是e^z的單葉性區域。例如，指數函式把直線x=x₀變為圓周，把直線y=y₀變為射線argw=y₀，因而把區域Sk變為區域0w<2π，把寬度為β的帶形區域α₀<α₀+β(β≤2π)變為開度為β的角形域α₀w<α₀+β。

復變對數函式

對數函式w=lnz是指數函式w=e^z的反函式，它有無窮多個值2kπ（k 為整數），稱為它的分支。每一個分支在區域θ₀z<θ₀+ 2π 中是解析的。對數函式把這個區域單葉地變為帶形區域θ₀w<θ₀+2π，也把開度為β的角形域θ₀z<θ₀+β(β≤2π)變為寬度為β的帶形區域θ₀w<θ₀+β。 像實對數函式一樣，它滿足lnz₁+lnz₂=ln(z₁·z₂)。

復變反三角函式

w=arcsinz，w=arccosz，w=arctanz分別是sinz，cosz和tanz的反函式，並稱復變反三角函式。它們能由對數函式合成。它們都是多值函式。

復變雙曲函式

將實雙曲函式推廣到複數域得復變雙曲函式。像實雙曲函式一樣，復變雙曲函式能由復變指數函式合成。

復變冪函式

將實冪函式的實變數用複數替換即得復變冪函式。一般來說，它是多值函式。

導數與微積分函式

一般初等函式的導數還是初等函式，但初等函式的不定積分不一定是初等函式。另外初等函式的反函式不一定是初等函式。