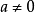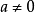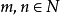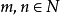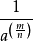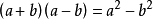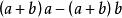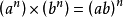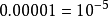乘方

求n個相同因數乘積的運算，叫做乘方，乘方的結果叫做冪(power)。其中，a叫做底數(base number)，n叫做指數(exponent)。當aⁿ看作a的n次乘方的結果時，也可讀作“a的n次冪”或“a的n次方”。

一個數都可以看作自己本身的一次方，指數1通常省略不寫。在寫分數和負數的n次方時要加括弧。四則運算順序：先乘方，再括弧（先小括弧，再中括弧，最後大括弧），接乘除，尾加減。

計算一個數的小數次方，如果那個小數是有理數，就把它化為 （即分數）的形式。特別的，除0以外的任何數的0次方均等於1。0的非正指數冪沒有意義。

基本介紹

• 中文名：乘方
• 外文名：involution;power
• 學科：數學
• 基本釋義：多個相同因數相乘的運算
• 表達：an
• 性質：除0以外的任何數的0次方等於1

定義

求n個相同因數乘積的運算，叫做乘方，乘方的結果叫做冪(power)。其中，a叫做底數(base number)，n叫做指數(exponent)，當aⁿ看作a的n次乘方的結果時，也可讀作“a的n次冪”或“a的n次方”。

註：下面的討論中，底數均不為0。

常用公式

同底數冪法則

同底數冪相乘除，原來的底數作底數，指數的和或差作指數。

例如：

1） ；

2） ；

3）

推導示例：

設 中，m=2，n=4，那么

=

=

=

=

正整數指數冪法則

，其中 *（即k為正整數）

指數為0冪法則

，其中 ， *

推導：

=

=

=1

負整數指數冪法則

，其中 ， *

推導：

=

=

=

正分數指數冪法則

，其中 ， ， *（即m,n為正整數）

負分數指數冪法則

，其中， ， ， ， *

推導：

=

=

=

=1/

=

分數指數冪時，當 *， 且 時，則該數在實數範圍內無意義

特別地，0的非正數指數冪沒有意義

平方差

兩數和乘兩數差等於它們的平方差。

用字母表示為：

推導：

=

=

=

分數的乘方法則

證明：

=

=

冪的乘方法則

冪的乘方，底數不變，指數相乘。

用字母表示為：

特別指出：

積的乘方

積的乘方，先把積中的每一個因數分別乘方，再把所得的冪相乘。

用字母表示為：

這個積的乘方法則也適用於三個以上乘數積的乘方。如：

同指數冪乘法

同指數冪相乘，指數不變，底數相乘。

用字母表示為：

完全平方

兩數和（或差）的平方，等於它們的平方的和加上（或者減去）它們的積的2倍。

用字母表示為：

我們一般把它叫作完全平方公式。

立方差

多項式平方

二項式

艾薩克·牛頓發現了二項式。二項式是乘方里的複雜運算。右圖為二項式計算法則。一般來說，二項式的各項係數按排列順序也可以這樣表示：

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…… …… ……

這就是著名的楊輝三角。

有理數乘方的符號法則

（1）負數的偶次冪是正數，負數的奇數冪是負數。

( 2)正數的任何次冪都是正數。

（3）0的任何正數次冪都是0。

速算

有些較特殊的數的平方，掌握規律後，可以使計算速度加快，現介紹如下。

由n個1組成的數的平方

我們觀察下面的例子。

1²=1

11²=121

111²=12321

1111²=1234321

11111²=123454321

111111²=12345654321

……

由以上例子可以看出這樣一個規律；求由n個1組成的數的平方，先由1寫到n，再由n寫到1，即：

11…1（n個1）²=1234…(n-1)n(n-1)…4321

注意：其中n只占一個數位，滿10應向前進位，當然，這樣的速算不宜位數過多。

由n個3組成的數的平方

我們仍觀察具體實例：

3²=9

33²=1089

333²=110889

3333²=11108889

33333²=1111088889

由此可知：

33…3（n個3）² = 11…11[(n-1)個1] 0 88…88[(n-1)個8] 9

個位是5的數的平方

把a看作10的個數，這樣個位數字是5的數的平方可以寫成；(10a+5)²的形式。根據完全平方式推導；

=

=

=

由此可知：個位數字是5的數的平方，等於去掉個位數字後，所得的數與比這個數大1的數相乘的積，後面再寫上25。

科學記數法

一個絕對值大於等於1的數可以寫成 （其中，，且n為正整數）的形式叫做科學記數法 例如： 、

當是負整數指數冪的時候，絕對值小於1的數也可以用科學記數法表示。例如： ，即絕對值小於1的數也可以用科學記數法表示為 的形式，其中 ， 是正整數。

任何非0實數的0次方都等於1。

pascal語言實現自然數乘方

注意:只能用於求底數、指數均為自然數,且冪不大於2147483647的乘方運算,否則會出錯.

var a,b,c,i:longint;{longint的範圍較大,為[-2147483648,2147483647]上所有整數}beginc:=1;{因為正整數的0次方均為1}readln(a,b);{輸入底數,指數}if (a=0) and (b=0) then writeln('無效輸入');{0的0次方無意義}for i:=1 to b do c:=c*a;{for循環實現計算c=a^b}writeln(c);{輸出c}end.