基本介紹
- 中文名:開方
- 外文名:rooting
- 解釋:一個數的方根的運算
- 類別:數學(代數)
- 適用範圍:數理科學
漢語釋義
- 數學術語。求方根的運算。對“乘方”而言。
《周髀算經》卷上“勾股圓方圖” 漢 趙君卿 註:“勾股各自乘,並之為弦實,開方除之,即弦也。” - 見方。
《南史·到溉傳》:“遭母憂,居喪盡禮。所處廬開方四尺,毀瘠過人。”
方根


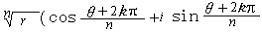 示例圖
示例圖方法
這個用兩個相同數字表示一個數的這個數字叫做開方
9=3x3 九等於三乘三
64=8x8
2,3,4,5,6,7,8,9,10就是4和9,16,25,36,49,64,81,100開方後的數
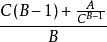
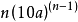






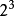


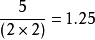






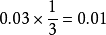
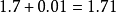

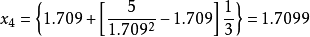

電腦程式代碼

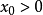


// 2015-12-24// By: ChenYu#include "math.h"#include "stdio.h"#define ABS(a) ((a)<0?-(a):(a))#ifdef _WIN32 typedef unsigned __int64 uint64;#else typedef unsigned long long uint64;#endif// calculate a approximate valuestatic double calcInitRoot(double x, int n){ const uint64 exptMask=((uint64)1<<11)-1; const uint64 fracMask=((uint64)1<<52)-1; uint64 xInt=*(uint64*)&x; int xExpt=(int)((xInt>>52)&exptMask)-1023; xInt=((uint64)((xExpt+1024*n-1)/n)<<52)+(xInt&fracMask)/n; return *(double*)&xInt;}double calcRoot(double x, int n){ int i, j, s=1-((x<0)<<(n&1)); double a=ABS(x); double x1, x0=calcInitRoot(a, n); double err=x0*1e-14; if(x==0) return 0; for(i=1; i<50; i++) { double xn=1; for(j=0; j<n-1; j++) xn*=x0; x1=((n-1)*x0*xn+a)/(xn*n); // printf("x%d=%.14f\n", i, x1); if(ABS(x1-x0)<=err) break; x0=x1; } return s*x1;}void main(){ double x=-31141.592653589793; int n=11; double y=calcRoot(x, n); printf("root(%g,%d)=%+.14f\n", x, n, y); printf("root(%g,%d)=%+.14f\n", x, n, pow(ABS(x), 1.0/n));}
