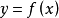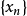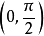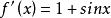切線法是通過曲線上的一些特徵點的切線的交點坐標關係來計算磁性體的產狀。
基本介紹
方程求根方法,收斂性的證明,計算實例,求方程實根,任意數開n次方,文學中的表現,股票術語,
方程求根方法
具體方法如下:


上述切線與 軸的交點為:
軸的交點為:



上面的疊代公式就是切線法的公式,不難看出這個公式實際就是牛頓公式。
(1) 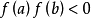
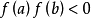
(2)  ;
;

(3) 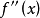 在
在 上恆正;
上恆正;
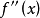

(4) 初值 應滿足
應滿足 。
。


收斂性的證明
下面給出牛頓切線法疊代格式收斂的充分條件,為了配合插圖,將充分條件具體表述為:
若(1)函式 在
在 上連續,且
上連續,且 ;
;



(2)在區間 上,
上, ,
, 。
。



則(1)方程 在區間
在區間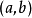 上存在唯一的實數根
上存在唯一的實數根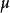 ;
;

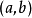
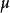
(2)取初值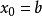 ,由疊代公式
,由疊代公式 (
( )定義的數列
)定義的數列 一定收斂,且
一定收斂,且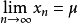 。
。
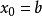



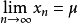

即曲線在過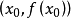 點的切線的上方,所以切線與
點的切線的上方,所以切線與 軸的交點
軸的交點 必滿足
必滿足 ,又因為
,又因為
 即
即 ,根據單調性可知
,根據單調性可知 。
。
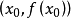







則 ,根據函式及導數的連續性可知
,根據函式及導數的連續性可知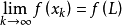 ,
, 。
。

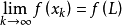

在疊代式 兩邊同求極限,可得
兩邊同求極限,可得 。從而可得
。從而可得 。
。



根據方程根的唯一性,可以斷定 就是方程
就是方程 在區間
在區間 上存在唯一的實數根
上存在唯一的實數根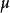 。
。



計算實例
求方程實根
求方程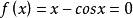 的實根。
的實根。
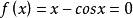
那么疊代公式為:
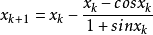
x0 | 1 |
x1 | 0.75036386784024 |
x2 | 0.73911289091136 |
x3 | 0.73908513338528 |
x4 | 0.73908513321516 |
x5 | 0.73908513321516 |
由此得到方程的實根為x=0.73908513321516...
上例的c語言程式代碼為:
#include "math.h"#include "stdio.h"#define ABS(a) ((a)<0?-(a):(a))static double f(double x){ return x-cos(x);}static double df(double x){ return 1+sin(x);}void main(){ int i; double x0=1, x1, err=1e-14; for(i=1; i<50; i++) { x1=x0-f(x0)/df(x0); printf("x[%d]=%.14f\n", i, x1); if(ABS(x1-x0)<err) break; x0=x1; }}任意數開n次方
設 ,那么
,那么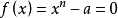 ,
,

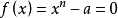

從而疊代公式為:
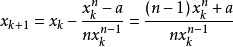
舉個例子:求

對應的疊代公式為: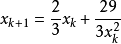
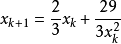
取初值x0=2,疊代如下:
x0 | 2 |
x1 | 3.75000000000000 |
x2 | 3.18740740740741 |
x3 | 3.07642248706644 |
x4 | 3.07232230248782 |
x5 | 3.07231682569561 |
x6 | 3.07231682568585 |
x7 | 3.07231682568585 |
從上面可以看出,只要疊代6次即可求出15位精度的近似值。
任意實數開n次方的c語言代碼為:
// 2015-12-24// By: ChenYu#include "math.h"#include "stdio.h"#define ABS(a) ((a)<0?-(a):(a))#ifdef _WIN32 typedef unsigned __int64 uint64;#else typedef unsigned long long uint64;#endif// calculate a approximate valuestatic double calcInitRoot(double x, int n){ const uint64 exptMask=((uint64)1<<11)-1; const uint64 fracMask=((uint64)1<<52)-1; uint64 xInt=*(uint64*)&x; int xExpt=(int)((xInt>>52)&exptMask)-1023; xInt=((uint64)((xExpt+1024*n-1)/n)<<52)+(xInt&fracMask)/n; return *(double*)&xInt;}double calcRoot(double x, int n){ int i, j, s=1-((x<0)<<(n&1)); double a=ABS(x); double x1, x0=calcInitRoot(a, n); double err=x0*1e-14; if(x==0) return 0; for(i=1; i<50; i++) { double xn=1; for(j=0; j<n-1; j++) xn*=x0; x1=((n-1)*x0*xn+a)/(xn*n);// printf("x%d=%.14f\n", i, x1); if(ABS(x1-x0)<=err) break; x0=x1; } return s*x1;}void main(){ double x=-31141.592653589793; int n=11; double y=calcRoot(x, n); printf("root(%g,%d)=%+.14f\n", x, n, y); printf("root(%g,%d)=%+.14f\n", x, n, pow(ABS(x), 1.0/n));}文學中的表現
清代小說《蕩寇志》中,出現了劉慧娘用切線法算仰角的情節。